total internal reflection

total internal reflection

by

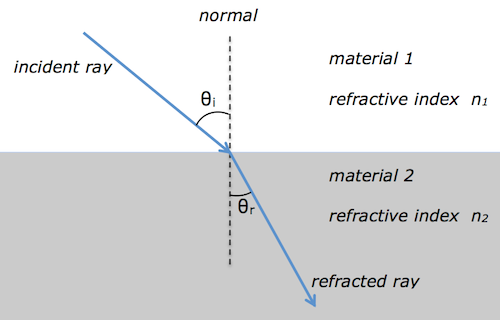
Earlier this week, we used semi-circular perspex blocks to investigate total internal reflection.

I’ve put together a short video showing total internal reflection in a semicircular block and a perspex model of an optical fibre.

total internal reflection from mr mackenzie on Vimeo.

There are some nice ray diagrams explaining total internal reflection on BBC Bitesize.

Cyberphysics has some examples of how optical fibers are used and the youtube video below shows how they can be used by doctors to see inside a patient’s body.

refraction, critical angle and total internal reflection

by

We met refraction during the National 5 course.  At Higher level, we are interested in the relationship between the angles of incidence θi and refraction θr.

Snell’s law tells us that

n_1\sin \theta_i = n_2 \sin \theta_r

Usually material 1 is air, and so n_1 = 1.  This simplifies Snell’s law to

\sin \theta_i = n \sin \theta_r

where n is the absolute refractive index of material 2.  Since the refractive index is equal to the ratio of the ray’s speed v in materials 1 & 2 and also equal to the ratio of the wave’s wavelength λ in materials 1 & 2, we can show that

n = \displaystyle {{{\sin \theta_i} \over  {\sin \theta_r}}} = \displaystyle {v_1 \over v_2} = \displaystyle {\lambda_1 \over \lambda_2}

Read more about Snells’s law here.

total internal reflection

total internal reflection from mr mackenzie on Vimeo.
The critical angle \theta_c and refractive index n are related by

\sin \theta_c = \displaystyle {1 \over n }

Here are some applications of total internal reflection here.  You can test your knowledge of refraction with this interactive simulation.

I have attached a pdf with some notes and questions on refraction, total internal reflection and critical angle.

Read

E-Book PDF: Open in New Window | Download