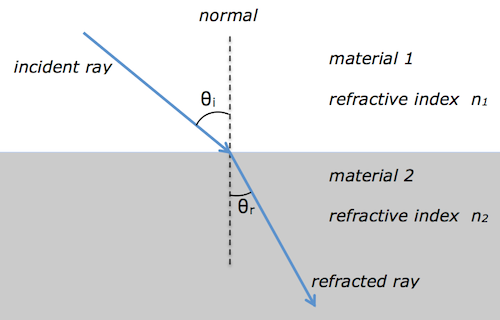
We met refraction during the National 5 course. At Higher level, we are interested in the relationship between the angles of incidence θi and refraction θr.
Snell’s law tells us that
Usually material 1 is air, and so . This simplifies Snell’s law to
where n is the absolute refractive index of material 2. Since the refractive index is equal to the ratio of the ray’s speed v in materials 1 & 2 and also equal to the ratio of the wave’s wavelength λ in materials 1 & 2, we can show that
Read more about Snells’s law here.
total internal reflection
Here are some applications of total internal reflection here. You can test your knowledge of refraction with this interactive simulation.
I have attached a pdf with some notes and questions on refraction, total internal reflection and critical angle.