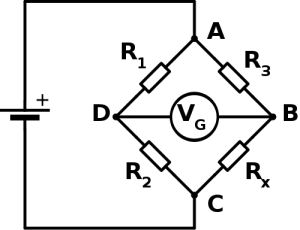
We’ve just completed the section of Higher unit 2 that investigates the behaviour of a Wheatstone Bridge. The bridge circuit is really just a pair of voltage dividers connected in parallel. A voltmeter, ammeter or galvanometer (very sensitive ammeter) connects the two voltage divider chains together, as shown below.
When the voltage (or current) displayed on the meter is zero, we say that the Wheatstone bridge is balanced. For a balanced bridge, it is possible to show that
[you have this proof in your notes folder]
For the circuit shown above, the voltmeter will display the difference in electrical potential between points B and D. We can calculate this potential difference by finding the voltages at points B and D using the voltage divider equation you used for Standard Grade/Intermediate 2 Physics.
So in this example,
and
The voltmeter displays the potential difference between these two points, i.e.
Here is a short video that provides a recap of the Wheatstone Bridge.
and a worked example from an old SQA past paper
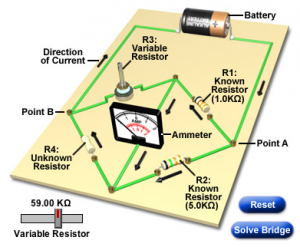
Now click on the picture below to try an interactive Wheatstone Bridge problem (you will need to have Java installed).
Instructions:
- Press the Reset button to change the value of all the resistors in the circuit.
- Use the slider to balance the bridge. The circuit uses a centre-zero meter, so aim to get the indicator dead centre.
- Find the unknown resistance (R4) using the value of the other 3 resistors when the circuit is balanced.
You can repeat this simulation as many times as you like by pressing Reset to change the resistor values…..it’s great practice!
Here is an example of an application of the Wheatstone Bridge, called the metre bridge.
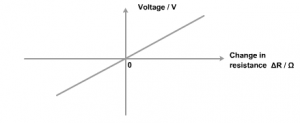
When a Wheatstone Bridge is slightly out of balance, it will provide a linear response. In other words, small changes in resistance will produce proportionally small changes in voltage or current. When these small changes are plotted, we obtain a straight line through the origin, like this:
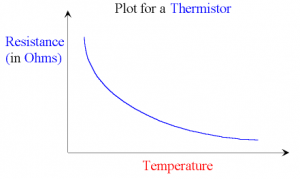
We tried to use this property of a Wheatstone Bridge to find the temperature of the physics classroom. We used some of the snow outside for a low temperature and boiling water for a high temperature.
As we discussed today, this was not a particularly successful experiment due to the non-linear response of the thermistor to changes in temperature – you might remember this from Standard Grade or Int 2 Physics.
For temperature ranges much smaller than the 100°C we attempted, it is possible to obtain an accurate estimate of room temperature.
Click on the download link below to try some Wheatstone Bridge questions.