refractive index

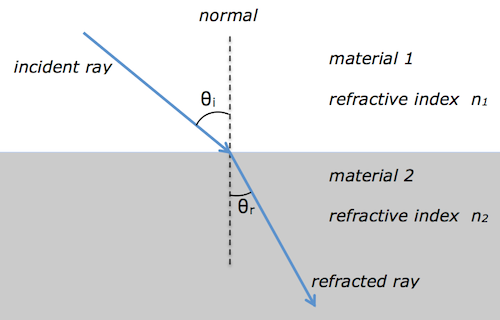
We met refraction during the National 5 course. At Higher level, we are interested in the relationship between the angles of incidence θi and refraction θr.

Snell’s law tells us that

$n_1\sin \theta_i = n_2 \sin \theta_r$

Usually material 1 is air, and so $n_1 = 1$ . This simplifies Snell’s law to

$\sin \theta_i = n \sin \theta_r$

where n is the absolute refractive index of material 2. Since the refractive index is equal to the ratio of the ray’s speed v in materials 1 & 2 and also equal to the ratio of the wave’s wavelength λ in materials 1 & 2, we can show that

$n = \displaystyle {{{\sin \theta_i} \over {\sin \theta_r}}} = \displaystyle {v_1 \over v_2} = \displaystyle {\lambda_1 \over \lambda_2}$