It’s complicated and cosmologists are not certain. One of the issues is only being able to see about 4% of the mass in the universe – the stars, planets, gas and dust. About 25% of the mass of the universe is Dark Matter. It’s “dark” because it doesn’t emit light that enables us to see it. Vera Rubin and Fritz Zwicky were the two astronomers who produced observations that led to the dark matter theory.
Vera Rubin measured star velocities in the Andromeda galaxy and plotted these against the star’s distance from the centre of the galaxy. Knowledge of rotational speeds within our Solar System would predict a graph similar to curve A. What she obtained was a relatively flat graph (B).
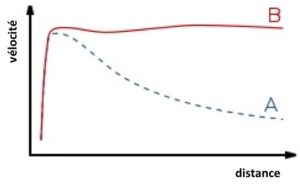 image from Quantum Diaries
image from Quantum Diaries
The rotational speed of the stars in curve B are far too fast for the Andromeda galaxy to stay together. The only explanation for the galaxy staying together was the presence of an awful lot of additional mass that couldn’t be detected. This new mass was named dark matter.
Rubin talks about her discovery in this video.
Vera Ruben dark matter dark energy from mr mackenzie on Vimeo.
Zwicky had been looking at clusters of galaxies, rather than individual stars within galaxies. He found something similar; the galaxies were swirling round at too great a speed and should fly apart.