
Solutions to SQA examination
1997 Higher Grade Physics
Paper II Solutions
Return to past paper index page.
1.a. Squaring the equation v = at gives:
v2 = a2t2 equation 1
The equation s = 1/2(at2) can be rearranged to give:
t2 = 2s/a which can be substituted into equation 1
v2 = a2(2s/a)
=>v2 = 2as
b.i. Funbalanced = Fthrust - Ffriction
Funbalanced = 3150 - 450
Funbalanced = 2700N
a = Funbalanced/m
a = 2700/1000
a = 2.7m/s/s
b.ii. To calculate the length of the track use : v2 = u2 + 2as
s = (v2 - u2)/2a
s = (332- 02)/2x2.7
s = 201.67m
c.
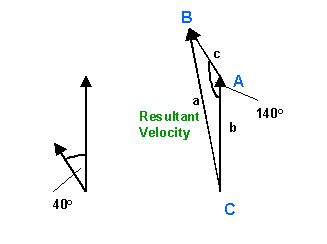 Use the cosine rule to calculate the resultant velocity,or,
draw an accurate scale diagram.
a2 = b2 + c2 -2bcCosA
a2 = 362 + 122 -2x36x12Cos140
a2 = 1296 + 144 - 864Cos140
a2 = 1296 + 144 - 864x-0.766
a2 = 2101.9
a = 45.8m/s
Use the sine rule to calculate angle C.
a/sinA = c/sinC
sinC = csinA/a
sinC = 12sin140o/45.8
sinC = 0.168
angle C = 9.7o
Resultant velocity = 45.8m/s with a bearing of 350.3o
2.a.i. Vhorizontal = Vcos36o
Vhorizontal = 41.7cos36o
Vhorizontal = 33.74m/s
a.ii. Vvertical = Vsin36o
Vvertical = 41.7sin36o
Vvertical = 24.5m/s
b. The time for the ball to reach Q(ttotal) can be calculated by summing
the time to travel from O to P(t1) and the time to travel from
P to Q(t2).
ttotal = t1 + t2
When P is reached the vertical component of the velocity is 0m/s.
This velocity is the final velocity(v) of the first part of the journey.
The initial component of the vertical velocity(u) for this part of the
journey is 24.5m/s.
v = 0m/s v = u +at1
u = 24.5m/s t1 = (v-u)/a
a = -9.8m/s/s t1 = (0-24.5)/-9.8
t1 = ? t1 = 2.5s
When falling from P to Q take the initial velocity(u) as 0m/s for
this part of the journey.
u = 0m/s s = ut2 + 1/2(at22)
s = -19.6m s = 1/2(at22)
a = -9.8m/s t22 = 2s/a
t2 = ? t22 = 2x-19.6/-9.8
t22 = 4
t2 = 2s
ttotal = t1 + t2
ttotal = 2.5 + 2
ttotal = 4.5s (As required)
c. Shorizontal = Vhorizontalxttotal
Shorizontal = 33.74x4.5
Shorizontal = 151.8m/s
3.a. Use the law of conservation of momentum to solve this problem.
Pbefore = Pafter
Before collision
Pbefore = mPuP + mQuQ
Pbefore = 0.2x0.5 + 0.3x0
Pbefore = 0.1kgm/s
After collision
Pafter = mPvP + mQvQ
0.1 = 0.2vP + 0.3x0.4
vP = (0.1 - 0.3x0.4)/0.2
vP = -0.1m/s The negative sign indicates the direction
is to the left.
b. DPp = Pp(after) - Pp(before)
Pp(after) = mPvP
Pp(after) = 0.2x-0.1
Pp(after) = -0.02kgm/s
Pp(before) = mPuP
Pp(before) = 0.2x0.5
Pp(before) = 0.1kgm/s
DPp = -0.02-0.1
DPp = -0.12kgm/s
c.i. Faveraget = mP(uP - vP)
Faverage = mP(uP - vP)/t
Faverage = 0.2[(0.5-(-0.1)]/0.06
Faverage = 2N
Note: the direction of this force is to the left.
c.ii.
Use the cosine rule to calculate the resultant velocity,or,
draw an accurate scale diagram.
a2 = b2 + c2 -2bcCosA
a2 = 362 + 122 -2x36x12Cos140
a2 = 1296 + 144 - 864Cos140
a2 = 1296 + 144 - 864x-0.766
a2 = 2101.9
a = 45.8m/s
Use the sine rule to calculate angle C.
a/sinA = c/sinC
sinC = csinA/a
sinC = 12sin140o/45.8
sinC = 0.168
angle C = 9.7o
Resultant velocity = 45.8m/s with a bearing of 350.3o
2.a.i. Vhorizontal = Vcos36o
Vhorizontal = 41.7cos36o
Vhorizontal = 33.74m/s
a.ii. Vvertical = Vsin36o
Vvertical = 41.7sin36o
Vvertical = 24.5m/s
b. The time for the ball to reach Q(ttotal) can be calculated by summing
the time to travel from O to P(t1) and the time to travel from
P to Q(t2).
ttotal = t1 + t2
When P is reached the vertical component of the velocity is 0m/s.
This velocity is the final velocity(v) of the first part of the journey.
The initial component of the vertical velocity(u) for this part of the
journey is 24.5m/s.
v = 0m/s v = u +at1
u = 24.5m/s t1 = (v-u)/a
a = -9.8m/s/s t1 = (0-24.5)/-9.8
t1 = ? t1 = 2.5s
When falling from P to Q take the initial velocity(u) as 0m/s for
this part of the journey.
u = 0m/s s = ut2 + 1/2(at22)
s = -19.6m s = 1/2(at22)
a = -9.8m/s t22 = 2s/a
t2 = ? t22 = 2x-19.6/-9.8
t22 = 4
t2 = 2s
ttotal = t1 + t2
ttotal = 2.5 + 2
ttotal = 4.5s (As required)
c. Shorizontal = Vhorizontalxttotal
Shorizontal = 33.74x4.5
Shorizontal = 151.8m/s
3.a. Use the law of conservation of momentum to solve this problem.
Pbefore = Pafter
Before collision
Pbefore = mPuP + mQuQ
Pbefore = 0.2x0.5 + 0.3x0
Pbefore = 0.1kgm/s
After collision
Pafter = mPvP + mQvQ
0.1 = 0.2vP + 0.3x0.4
vP = (0.1 - 0.3x0.4)/0.2
vP = -0.1m/s The negative sign indicates the direction
is to the left.
b. DPp = Pp(after) - Pp(before)
Pp(after) = mPvP
Pp(after) = 0.2x-0.1
Pp(after) = -0.02kgm/s
Pp(before) = mPuP
Pp(before) = 0.2x0.5
Pp(before) = 0.1kgm/s
DPp = -0.02-0.1
DPp = -0.12kgm/s
c.i. Faveraget = mP(uP - vP)
Faverage = mP(uP - vP)/t
Faverage = 0.2[(0.5-(-0.1)]/0.06
Faverage = 2N
Note: the direction of this force is to the left.
c.ii.
 4.a. The assumption in this experiment is that the gas in the container
is the same as the water temperature. To facilitate this the can
must be fully immersed to allow the gas and water temperature to
equilibrate.
b. P1 = 100kPa
T1 = (17+273)K = 290K
P2 = ?
T2 = (75+273)K = 348K
P1/T1 = P2/T2
P2 = P1T2/T1
P2 = 100x348/290
P2 = 120kPa
c. P = F/A
F = PA
F = 120x103x0.001
F = 120N
d. The mass and the volume of gas are fixed in this experiment,therefore,
the density(mass/volume) must also remain constant.
5.a. A battery emf of 12V will supply 12J of energy to each coulomb
of charge passing through the cell.
b.i. P = V2/R
R = V2/P
R = 122/48
R = 3W
b.ii. When S1 is closed the circuit can be treated as a simple series
circuit with the internal resistor(r) in series with the headlamp
resistance(Rh).
Rtotal = Rh + r
Rtotal = 3 + 0.05
Rtotal = 3.05W
I = emf/Rtotal
I = 12/3.05
I = 3.93A
Vheadlamp = IRh
Vheadlamp = 3.93x3
Vheadlamp = 11.8V (as required)
c.i. The bulb and the starter motor are in parallel. The resistance of this
network Rp is calculated as shown below:
1/Rp = 1/Rbulb + 1/Rmotor
1/Rp = 1/3 + 1/0.12
1/Rp = 8.66...
Rp = 0.1154W
Rtotal = Rp + r
Rtotal = 0.115 + 0.05
Rtotal = 0.165W
c.ii. I = emf/Rtotal
I = 12/0.165
I = 72.7A
6.a.i. Gain = Voutput/Vinput
Gain = -9x30mv/5x2mV
Gain = -270mV/10mv
Gain = 27
a.ii. Vpeak = 1.414Vrms
Vrms = Vpeak/1.414
Vrms = 190.9mV
a.iii.Gain = Voutput/Vinput =-Rf/R1
To produce a gain of magnitude 27 choose:
Rf = 270kW
R1 = 10kW
Other values are acceptable as long as the ratio of Rf to R1
is 27.
b.i. The bridge is balanced when the digital voltmeter reads 0V.
This means the potential at X and Y are equal and there is
no potential difference between these points.
b.ii. Voutput = (-Rf/R-)(V--V+)
(V--V+) = -Voutput(R-/Rf)
(V--V+) = -(-0.18)(100x103/1x106)
(V--V+) = 0.18(0.1)
(V--V+) = 0.018V
VY-VX = 0.018V
b.iii.At 20oC the potential at Y(VY) falls to a value less than it was
when the bridge was balanced at 23oC.
As VY is less than VX => VY-VX is negative.
=> Voutput=(-Rf/R-)(VY-VX)
Voutput= positive value.
Note: If the resistance of the thermistor varies linearly with temperature in
range 20oC to 26oC the output voltage at 20oC will be +0.18V.
7.a.i. All the supply voltage is across the resistor at the instant the switch
is closed. At this instant Vsupply = Vresistor.
I = 100x10-6
R = 150,000W
Vresistor = ?
Vresistor = IRresistor
Vresistor = 100x10-6x150000
Vresistor = 15V
Vsupply = Vresistor = 15V
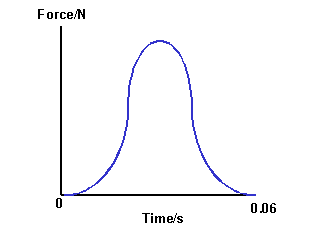
a.ii. The current in the circuit must first be calculated when the voltage
across the resistor is 6V.
I = ?
Vresistor = 6V
R = 150,000W
I = V/R
I = 6/150000
I = 40x10-6A = 40mA
From the graph read the time when the current is 40mA.
Time = 40s
a.iii.Vsupply = Vresistor + Vcapacitor
Vcapacitor = Vsupply - Vresistor
Vcapacitor = 15 - 6
Vcapacitor = 9V
b.i.A Q = CV
C = 16mF = 16x10-6
V = 6kV = 6000V (This is the voltage across the capacitor when fully charged)
Q = ?
Q = 16x10-6 x 6000
Q = 0.096C
b.i.B E = 1/2(QV)
E = 1/2(0.096X6000)
E = 288J
b.ii. I = Q/t
I = 0.096/2x10-3
I = 48A
8.a.i. A maxima occurs when two waves interfere constructively. This happens
when waves are in phase.
A minima occurs when two waves interfere destructively. This happens when
the two waves are 180o out of phase.
a.ii.
4.a. The assumption in this experiment is that the gas in the container
is the same as the water temperature. To facilitate this the can
must be fully immersed to allow the gas and water temperature to
equilibrate.
b. P1 = 100kPa
T1 = (17+273)K = 290K
P2 = ?
T2 = (75+273)K = 348K
P1/T1 = P2/T2
P2 = P1T2/T1
P2 = 100x348/290
P2 = 120kPa
c. P = F/A
F = PA
F = 120x103x0.001
F = 120N
d. The mass and the volume of gas are fixed in this experiment,therefore,
the density(mass/volume) must also remain constant.
5.a. A battery emf of 12V will supply 12J of energy to each coulomb
of charge passing through the cell.
b.i. P = V2/R
R = V2/P
R = 122/48
R = 3W
b.ii. When S1 is closed the circuit can be treated as a simple series
circuit with the internal resistor(r) in series with the headlamp
resistance(Rh).
Rtotal = Rh + r
Rtotal = 3 + 0.05
Rtotal = 3.05W
I = emf/Rtotal
I = 12/3.05
I = 3.93A
Vheadlamp = IRh
Vheadlamp = 3.93x3
Vheadlamp = 11.8V (as required)
c.i. The bulb and the starter motor are in parallel. The resistance of this
network Rp is calculated as shown below:
1/Rp = 1/Rbulb + 1/Rmotor
1/Rp = 1/3 + 1/0.12
1/Rp = 8.66...
Rp = 0.1154W
Rtotal = Rp + r
Rtotal = 0.115 + 0.05
Rtotal = 0.165W
c.ii. I = emf/Rtotal
I = 12/0.165
I = 72.7A
6.a.i. Gain = Voutput/Vinput
Gain = -9x30mv/5x2mV
Gain = -270mV/10mv
Gain = 27
a.ii. Vpeak = 1.414Vrms
Vrms = Vpeak/1.414
Vrms = 190.9mV
a.iii.Gain = Voutput/Vinput =-Rf/R1
To produce a gain of magnitude 27 choose:
Rf = 270kW
R1 = 10kW
Other values are acceptable as long as the ratio of Rf to R1
is 27.
b.i. The bridge is balanced when the digital voltmeter reads 0V.
This means the potential at X and Y are equal and there is
no potential difference between these points.
b.ii. Voutput = (-Rf/R-)(V--V+)
(V--V+) = -Voutput(R-/Rf)
(V--V+) = -(-0.18)(100x103/1x106)
(V--V+) = 0.18(0.1)
(V--V+) = 0.018V
VY-VX = 0.018V
b.iii.At 20oC the potential at Y(VY) falls to a value less than it was
when the bridge was balanced at 23oC.
As VY is less than VX => VY-VX is negative.
=> Voutput=(-Rf/R-)(VY-VX)
Voutput= positive value.
Note: If the resistance of the thermistor varies linearly with temperature in
range 20oC to 26oC the output voltage at 20oC will be +0.18V.
7.a.i. All the supply voltage is across the resistor at the instant the switch
is closed. At this instant Vsupply = Vresistor.
I = 100x10-6
R = 150,000W
Vresistor = ?
Vresistor = IRresistor
Vresistor = 100x10-6x150000
Vresistor = 15V
Vsupply = Vresistor = 15V
a.ii. The current in the circuit must first be calculated when the voltage
across the resistor is 6V.
I = ?
Vresistor = 6V
R = 150,000W
I = V/R
I = 6/150000
I = 40x10-6A = 40mA
From the graph read the time when the current is 40mA.
Time = 40s
a.iii.Vsupply = Vresistor + Vcapacitor
Vcapacitor = Vsupply - Vresistor
Vcapacitor = 15 - 6
Vcapacitor = 9V
b.i.A Q = CV
C = 16mF = 16x10-6
V = 6kV = 6000V (This is the voltage across the capacitor when fully charged)
Q = ?
Q = 16x10-6 x 6000
Q = 0.096C
b.i.B E = 1/2(QV)
E = 1/2(0.096X6000)
E = 288J
b.ii. I = Q/t
I = 0.096/2x10-3
I = 48A
8.a.i. A maxima occurs when two waves interfere constructively. This happens
when waves are in phase.
A minima occurs when two waves interfere destructively. This happens when
the two waves are 180o out of phase.
a.ii.
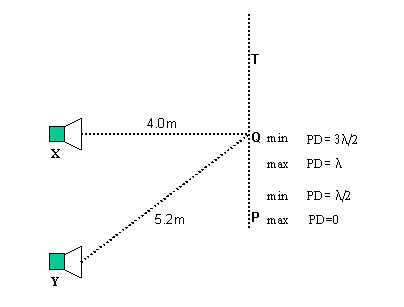 The minima is produced when the path difference YQ-XQ is equal to 3/2l.
YQ-XQ = (5.2-4.0)m = 1.2m
YQ-XQ = 3/2l
l=(2x1.2)/3
l = 0.8m
b.i. The speed of sound is constant in air, therefore increasing the frequency
will decrease the wavelength. If the frequency is increased by a factor of
5 the wavelength will decrease by a factor of 5.
Wavelength at 1000Hz = 1.2/5 = 0.24m
b.ii. If the path difference is fixed at 1.2m this will represent a whole
number of wavelengths for certain frequencies and produce maxima, however,
for other frequencies this will represent a whole number of half wavelengths
and produce minima. For this reason a series of maxima and minima are produced.
9.a. nplastic = sinqair/sinqplastic
nplastic = sin15o/sin10o (Note that it is the angle between the ray
and the normal that must be used.)
nplastic = 1.49
b.i. qcrit = sin-1(1/nglass)
qcrit = sin-1(1/1.44)
qcrit = sin-1(0.694)
qcrit = 44.0o
b.ii. Ray Q will be refracted and partially reflected.
Ray P will be totally internally reflected because the incident angle
of 45o is greater than the critical angle.
The minima is produced when the path difference YQ-XQ is equal to 3/2l.
YQ-XQ = (5.2-4.0)m = 1.2m
YQ-XQ = 3/2l
l=(2x1.2)/3
l = 0.8m
b.i. The speed of sound is constant in air, therefore increasing the frequency
will decrease the wavelength. If the frequency is increased by a factor of
5 the wavelength will decrease by a factor of 5.
Wavelength at 1000Hz = 1.2/5 = 0.24m
b.ii. If the path difference is fixed at 1.2m this will represent a whole
number of wavelengths for certain frequencies and produce maxima, however,
for other frequencies this will represent a whole number of half wavelengths
and produce minima. For this reason a series of maxima and minima are produced.
9.a. nplastic = sinqair/sinqplastic
nplastic = sin15o/sin10o (Note that it is the angle between the ray
and the normal that must be used.)
nplastic = 1.49
b.i. qcrit = sin-1(1/nglass)
qcrit = sin-1(1/1.44)
qcrit = sin-1(0.694)
qcrit = 44.0o
b.ii. Ray Q will be refracted and partially reflected.
Ray P will be totally internally reflected because the incident angle
of 45o is greater than the critical angle.
 10.a.i.
10.a.i.
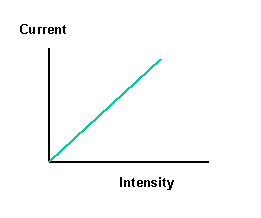 a.ii. Individual electrons in the metal atom absorb the energy of a single
photon, the energy of which is dependent on the frequency of the photon.
The photon energy can be calculated using the equation E = hf. Below
a certain frequency the energy absorbed by an electronin the metal, from
the photon, is below that required to escape from the metal atom, thus
the current in the circuit will be zero.
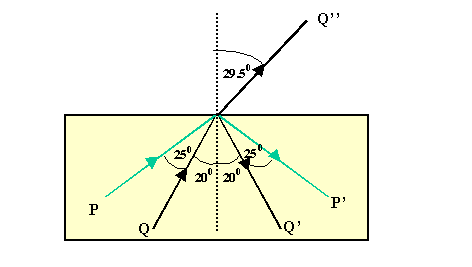
b.i. The threshold frequency will provide electrons with just enough
energy to overcome the work function of the metal and eject electrons
with no excess kinetic energy. Thus to estimate the work function from the
graph the line must be extrapolated until it cuts the x-axis of the
graph.
X-axis intercept = 6.7x1014Hz
This is the threshold frequency.
b.ii. The work function is calculated using:
Ework function = hfthreshold
Ework function = 6.63x10-34x6.6x1014
Ework function = 4.4x10-19J
This is closest to the work function of the metal calcium
11.a. Alpha particles have a positive charge. It was therefore concluded
that electrostatic repulsion from a like charge, of very large mass,
was required to produce a large angle deflection. However, as large
angle deflections were very rare, and most alpha particles were
undeviated from their original path, it led Rutherford to conclude
that most of the atom was empty space with the large positive mass
concentrated at the centre of the atom.
b.i. The total dose equivalent received is calculated using the equation:
H =QD.
Hgamma = QgammaDgamma
Hgamma = 1x200
Hgamma = 200mSv
Hneutrons = QneutronsDneutrons
Hneutrons = 3x100
Hneutrons = 300mSv
Htotal = Hgamma + Hneutrons
Htotal = 200 + 300
Htotal = 500mSv
b.ii.
a.ii. Individual electrons in the metal atom absorb the energy of a single
photon, the energy of which is dependent on the frequency of the photon.
The photon energy can be calculated using the equation E = hf. Below
a certain frequency the energy absorbed by an electronin the metal, from
the photon, is below that required to escape from the metal atom, thus
the current in the circuit will be zero.
b.i. The threshold frequency will provide electrons with just enough
energy to overcome the work function of the metal and eject electrons
with no excess kinetic energy. Thus to estimate the work function from the
graph the line must be extrapolated until it cuts the x-axis of the
graph.
X-axis intercept = 6.7x1014Hz
This is the threshold frequency.
b.ii. The work function is calculated using:
Ework function = hfthreshold
Ework function = 6.63x10-34x6.6x1014
Ework function = 4.4x10-19J
This is closest to the work function of the metal calcium
11.a. Alpha particles have a positive charge. It was therefore concluded
that electrostatic repulsion from a like charge, of very large mass,
was required to produce a large angle deflection. However, as large
angle deflections were very rare, and most alpha particles were
undeviated from their original path, it led Rutherford to conclude
that most of the atom was empty space with the large positive mass
concentrated at the centre of the atom.
b.i. The total dose equivalent received is calculated using the equation:
H =QD.
Hgamma = QgammaDgamma
Hgamma = 1x200
Hgamma = 200mSv
Hneutrons = QneutronsDneutrons
Hneutrons = 3x100
Hneutrons = 300mSv
Htotal = Hgamma + Hneutrons
Htotal = 200 + 300
Htotal = 500mSv
b.ii.
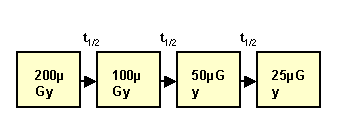 Three half value thicknesses are required.
3t1/2 = 3x8 = 24mm
Three half value thicknesses are required.
3t1/2 = 3x8 = 24mm
END OF QUESTION PAPER
Return to past paper index page.


 Use the cosine rule to calculate the resultant velocity,or,
draw an accurate scale diagram.
a2 = b2 + c2 -2bcCosA
a2 = 362 + 122 -2x36x12Cos140
a2 = 1296 + 144 - 864Cos140
a2 = 1296 + 144 - 864x-0.766
a2 = 2101.9
a = 45.8m/s
Use the sine rule to calculate angle C.
a/sinA = c/sinC
sinC = csinA/a
sinC = 12sin140o/45.8
sinC = 0.168
angle C = 9.7o
Resultant velocity = 45.8m/s with a bearing of 350.3o
2.a.i. Vhorizontal = Vcos36o
Vhorizontal = 41.7cos36o
Vhorizontal = 33.74m/s
a.ii. Vvertical = Vsin36o
Vvertical = 41.7sin36o
Vvertical = 24.5m/s
b. The time for the ball to reach Q(ttotal) can be calculated by summing
the time to travel from O to P(t1) and the time to travel from
P to Q(t2).
ttotal = t1 + t2
When P is reached the vertical component of the velocity is 0m/s.
This velocity is the final velocity(v) of the first part of the journey.
The initial component of the vertical velocity(u) for this part of the
journey is 24.5m/s.
v = 0m/s v = u +at1
u = 24.5m/s t1 = (v-u)/a
a = -9.8m/s/s t1 = (0-24.5)/-9.8
t1 = ? t1 = 2.5s
When falling from P to Q take the initial velocity(u) as 0m/s for
this part of the journey.
u = 0m/s s = ut2 + 1/2(at22)
s = -19.6m s = 1/2(at22)
a = -9.8m/s t22 = 2s/a
t2 = ? t22 = 2x-19.6/-9.8
t22 = 4
t2 = 2s
ttotal = t1 + t2
ttotal = 2.5 + 2
ttotal = 4.5s (As required)
c. Shorizontal = Vhorizontalxttotal
Shorizontal = 33.74x4.5
Shorizontal = 151.8m/s
3.a. Use the law of conservation of momentum to solve this problem.
Pbefore = Pafter
Before collision
Pbefore = mPuP + mQuQ
Pbefore = 0.2x0.5 + 0.3x0
Pbefore = 0.1kgm/s
After collision
Pafter = mPvP + mQvQ
0.1 = 0.2vP + 0.3x0.4
vP = (0.1 - 0.3x0.4)/0.2
vP = -0.1m/s The negative sign indicates the direction
is to the left.
b. DPp = Pp(after) - Pp(before)
Pp(after) = mPvP
Pp(after) = 0.2x-0.1
Pp(after) = -0.02kgm/s
Pp(before) = mPuP
Pp(before) = 0.2x0.5
Pp(before) = 0.1kgm/s
DPp = -0.02-0.1
DPp = -0.12kgm/s
c.i. Faveraget = mP(uP - vP)
Faverage = mP(uP - vP)/t
Faverage = 0.2[(0.5-(-0.1)]/0.06
Faverage = 2N
Note: the direction of this force is to the left.
c.ii.
Use the cosine rule to calculate the resultant velocity,or,
draw an accurate scale diagram.
a2 = b2 + c2 -2bcCosA
a2 = 362 + 122 -2x36x12Cos140
a2 = 1296 + 144 - 864Cos140
a2 = 1296 + 144 - 864x-0.766
a2 = 2101.9
a = 45.8m/s
Use the sine rule to calculate angle C.
a/sinA = c/sinC
sinC = csinA/a
sinC = 12sin140o/45.8
sinC = 0.168
angle C = 9.7o
Resultant velocity = 45.8m/s with a bearing of 350.3o
2.a.i. Vhorizontal = Vcos36o
Vhorizontal = 41.7cos36o
Vhorizontal = 33.74m/s
a.ii. Vvertical = Vsin36o
Vvertical = 41.7sin36o
Vvertical = 24.5m/s
b. The time for the ball to reach Q(ttotal) can be calculated by summing
the time to travel from O to P(t1) and the time to travel from
P to Q(t2).
ttotal = t1 + t2
When P is reached the vertical component of the velocity is 0m/s.
This velocity is the final velocity(v) of the first part of the journey.
The initial component of the vertical velocity(u) for this part of the
journey is 24.5m/s.
v = 0m/s v = u +at1
u = 24.5m/s t1 = (v-u)/a
a = -9.8m/s/s t1 = (0-24.5)/-9.8
t1 = ? t1 = 2.5s
When falling from P to Q take the initial velocity(u) as 0m/s for
this part of the journey.
u = 0m/s s = ut2 + 1/2(at22)
s = -19.6m s = 1/2(at22)
a = -9.8m/s t22 = 2s/a
t2 = ? t22 = 2x-19.6/-9.8
t22 = 4
t2 = 2s
ttotal = t1 + t2
ttotal = 2.5 + 2
ttotal = 4.5s (As required)
c. Shorizontal = Vhorizontalxttotal
Shorizontal = 33.74x4.5
Shorizontal = 151.8m/s
3.a. Use the law of conservation of momentum to solve this problem.
Pbefore = Pafter
Before collision
Pbefore = mPuP + mQuQ
Pbefore = 0.2x0.5 + 0.3x0
Pbefore = 0.1kgm/s
After collision
Pafter = mPvP + mQvQ
0.1 = 0.2vP + 0.3x0.4
vP = (0.1 - 0.3x0.4)/0.2
vP = -0.1m/s The negative sign indicates the direction
is to the left.
b. DPp = Pp(after) - Pp(before)
Pp(after) = mPvP
Pp(after) = 0.2x-0.1
Pp(after) = -0.02kgm/s
Pp(before) = mPuP
Pp(before) = 0.2x0.5
Pp(before) = 0.1kgm/s
DPp = -0.02-0.1
DPp = -0.12kgm/s
c.i. Faveraget = mP(uP - vP)
Faverage = mP(uP - vP)/t
Faverage = 0.2[(0.5-(-0.1)]/0.06
Faverage = 2N
Note: the direction of this force is to the left.
c.ii.
 4.a. The assumption in this experiment is that the gas in the container
is the same as the water temperature. To facilitate this the can
must be fully immersed to allow the gas and water temperature to
equilibrate.
b. P1 = 100kPa
T1 = (17+273)K = 290K
P2 = ?
T2 = (75+273)K = 348K
P1/T1 = P2/T2
P2 = P1T2/T1
P2 = 100x348/290
P2 = 120kPa
c. P = F/A
F = PA
F = 120x103x0.001
F = 120N
d. The mass and the volume of gas are fixed in this experiment,therefore,
the density(mass/volume) must also remain constant.
5.a. A battery emf of 12V will supply 12J of energy to each coulomb
of charge passing through the cell.
b.i. P = V2/R
R = V2/P
R = 122/48
R = 3W
b.ii. When S1 is closed the circuit can be treated as a simple series
circuit with the internal resistor(r) in series with the headlamp
resistance(Rh).
Rtotal = Rh + r
Rtotal = 3 + 0.05
Rtotal = 3.05W
I = emf/Rtotal
I = 12/3.05
I = 3.93A
Vheadlamp = IRh
Vheadlamp = 3.93x3
Vheadlamp = 11.8V (as required)
c.i. The bulb and the starter motor are in parallel. The resistance of this
network Rp is calculated as shown below:
1/Rp = 1/Rbulb + 1/Rmotor
1/Rp = 1/3 + 1/0.12
1/Rp = 8.66...
Rp = 0.1154W
Rtotal = Rp + r
Rtotal = 0.115 + 0.05
Rtotal = 0.165W
c.ii. I = emf/Rtotal
I = 12/0.165
I = 72.7A
6.a.i. Gain = Voutput/Vinput
Gain = -9x30mv/5x2mV
Gain = -270mV/10mv
Gain = 27
a.ii. Vpeak = 1.414Vrms
Vrms = Vpeak/1.414
Vrms = 190.9mV
a.iii.Gain = Voutput/Vinput =-Rf/R1
To produce a gain of magnitude 27 choose:
Rf = 270kW
R1 = 10kW
Other values are acceptable as long as the ratio of Rf to R1
is 27.
b.i. The bridge is balanced when the digital voltmeter reads 0V.
This means the potential at X and Y are equal and there is
no potential difference between these points.
b.ii. Voutput = (-Rf/R-)(V--V+)
(V--V+) = -Voutput(R-/Rf)
(V--V+) = -(-0.18)(100x103/1x106)
(V--V+) = 0.18(0.1)
(V--V+) = 0.018V
VY-VX = 0.018V
b.iii.At 20oC the potential at Y(VY) falls to a value less than it was
when the bridge was balanced at 23oC.
As VY is less than VX => VY-VX is negative.
=> Voutput=(-Rf/R-)(VY-VX)
Voutput= positive value.
Note: If the resistance of the thermistor varies linearly with temperature in
range 20oC to 26oC the output voltage at 20oC will be +0.18V.
7.a.i. All the supply voltage is across the resistor at the instant the switch
is closed. At this instant Vsupply = Vresistor.
I = 100x10-6
R = 150,000W
Vresistor = ?
Vresistor = IRresistor
Vresistor = 100x10-6x150000
Vresistor = 15V
Vsupply = Vresistor = 15V
a.ii. The current in the circuit must first be calculated when the voltage
across the resistor is 6V.
I = ?
Vresistor = 6V
R = 150,000W
I = V/R
I = 6/150000
I = 40x10-6A = 40mA
From the graph read the time when the current is 40mA.
Time = 40s
a.iii.Vsupply = Vresistor + Vcapacitor
Vcapacitor = Vsupply - Vresistor
Vcapacitor = 15 - 6
Vcapacitor = 9V
b.i.A Q = CV
C = 16mF = 16x10-6
V = 6kV = 6000V (This is the voltage across the capacitor when fully charged)
Q = ?
Q = 16x10-6 x 6000
Q = 0.096C
b.i.B E = 1/2(QV)
E = 1/2(0.096X6000)
E = 288J
b.ii. I = Q/t
I = 0.096/2x10-3
I = 48A
8.a.i. A maxima occurs when two waves interfere constructively. This happens
when waves are in phase.
A minima occurs when two waves interfere destructively. This happens when
the two waves are 180o out of phase.
a.ii.
4.a. The assumption in this experiment is that the gas in the container
is the same as the water temperature. To facilitate this the can
must be fully immersed to allow the gas and water temperature to
equilibrate.
b. P1 = 100kPa
T1 = (17+273)K = 290K
P2 = ?
T2 = (75+273)K = 348K
P1/T1 = P2/T2
P2 = P1T2/T1
P2 = 100x348/290
P2 = 120kPa
c. P = F/A
F = PA
F = 120x103x0.001
F = 120N
d. The mass and the volume of gas are fixed in this experiment,therefore,
the density(mass/volume) must also remain constant.
5.a. A battery emf of 12V will supply 12J of energy to each coulomb
of charge passing through the cell.
b.i. P = V2/R
R = V2/P
R = 122/48
R = 3W
b.ii. When S1 is closed the circuit can be treated as a simple series
circuit with the internal resistor(r) in series with the headlamp
resistance(Rh).
Rtotal = Rh + r
Rtotal = 3 + 0.05
Rtotal = 3.05W
I = emf/Rtotal
I = 12/3.05
I = 3.93A
Vheadlamp = IRh
Vheadlamp = 3.93x3
Vheadlamp = 11.8V (as required)
c.i. The bulb and the starter motor are in parallel. The resistance of this
network Rp is calculated as shown below:
1/Rp = 1/Rbulb + 1/Rmotor
1/Rp = 1/3 + 1/0.12
1/Rp = 8.66...
Rp = 0.1154W
Rtotal = Rp + r
Rtotal = 0.115 + 0.05
Rtotal = 0.165W
c.ii. I = emf/Rtotal
I = 12/0.165
I = 72.7A
6.a.i. Gain = Voutput/Vinput
Gain = -9x30mv/5x2mV
Gain = -270mV/10mv
Gain = 27
a.ii. Vpeak = 1.414Vrms
Vrms = Vpeak/1.414
Vrms = 190.9mV
a.iii.Gain = Voutput/Vinput =-Rf/R1
To produce a gain of magnitude 27 choose:
Rf = 270kW
R1 = 10kW
Other values are acceptable as long as the ratio of Rf to R1
is 27.
b.i. The bridge is balanced when the digital voltmeter reads 0V.
This means the potential at X and Y are equal and there is
no potential difference between these points.
b.ii. Voutput = (-Rf/R-)(V--V+)
(V--V+) = -Voutput(R-/Rf)
(V--V+) = -(-0.18)(100x103/1x106)
(V--V+) = 0.18(0.1)
(V--V+) = 0.018V
VY-VX = 0.018V
b.iii.At 20oC the potential at Y(VY) falls to a value less than it was
when the bridge was balanced at 23oC.
As VY is less than VX => VY-VX is negative.
=> Voutput=(-Rf/R-)(VY-VX)
Voutput= positive value.
Note: If the resistance of the thermistor varies linearly with temperature in
range 20oC to 26oC the output voltage at 20oC will be +0.18V.
7.a.i. All the supply voltage is across the resistor at the instant the switch
is closed. At this instant Vsupply = Vresistor.
I = 100x10-6
R = 150,000W
Vresistor = ?
Vresistor = IRresistor
Vresistor = 100x10-6x150000
Vresistor = 15V
Vsupply = Vresistor = 15V
a.ii. The current in the circuit must first be calculated when the voltage
across the resistor is 6V.
I = ?
Vresistor = 6V
R = 150,000W
I = V/R
I = 6/150000
I = 40x10-6A = 40mA
From the graph read the time when the current is 40mA.
Time = 40s
a.iii.Vsupply = Vresistor + Vcapacitor
Vcapacitor = Vsupply - Vresistor
Vcapacitor = 15 - 6
Vcapacitor = 9V
b.i.A Q = CV
C = 16mF = 16x10-6
V = 6kV = 6000V (This is the voltage across the capacitor when fully charged)
Q = ?
Q = 16x10-6 x 6000
Q = 0.096C
b.i.B E = 1/2(QV)
E = 1/2(0.096X6000)
E = 288J
b.ii. I = Q/t
I = 0.096/2x10-3
I = 48A
8.a.i. A maxima occurs when two waves interfere constructively. This happens
when waves are in phase.
A minima occurs when two waves interfere destructively. This happens when
the two waves are 180o out of phase.
a.ii.
 The minima is produced when the path difference YQ-XQ is equal to 3/2l.
YQ-XQ = (5.2-4.0)m = 1.2m
YQ-XQ = 3/2l
l=(2x1.2)/3
l = 0.8m
b.i. The speed of sound is constant in air, therefore increasing the frequency
will decrease the wavelength. If the frequency is increased by a factor of
5 the wavelength will decrease by a factor of 5.
Wavelength at 1000Hz = 1.2/5 = 0.24m
b.ii. If the path difference is fixed at 1.2m this will represent a whole
number of wavelengths for certain frequencies and produce maxima, however,
for other frequencies this will represent a whole number of half wavelengths
and produce minima. For this reason a series of maxima and minima are produced.
9.a. nplastic = sinqair/sinqplastic
nplastic = sin15o/sin10o (Note that it is the angle between the ray
and the normal that must be used.)
nplastic = 1.49
b.i. qcrit = sin-1(1/nglass)
qcrit = sin-1(1/1.44)
qcrit = sin-1(0.694)
qcrit = 44.0o
b.ii. Ray Q will be refracted and partially reflected.
Ray P will be totally internally reflected because the incident angle
of 45o is greater than the critical angle.
The minima is produced when the path difference YQ-XQ is equal to 3/2l.
YQ-XQ = (5.2-4.0)m = 1.2m
YQ-XQ = 3/2l
l=(2x1.2)/3
l = 0.8m
b.i. The speed of sound is constant in air, therefore increasing the frequency
will decrease the wavelength. If the frequency is increased by a factor of
5 the wavelength will decrease by a factor of 5.
Wavelength at 1000Hz = 1.2/5 = 0.24m
b.ii. If the path difference is fixed at 1.2m this will represent a whole
number of wavelengths for certain frequencies and produce maxima, however,
for other frequencies this will represent a whole number of half wavelengths
and produce minima. For this reason a series of maxima and minima are produced.
9.a. nplastic = sinqair/sinqplastic
nplastic = sin15o/sin10o (Note that it is the angle between the ray
and the normal that must be used.)
nplastic = 1.49
b.i. qcrit = sin-1(1/nglass)
qcrit = sin-1(1/1.44)
qcrit = sin-1(0.694)
qcrit = 44.0o
b.ii. Ray Q will be refracted and partially reflected.
Ray P will be totally internally reflected because the incident angle
of 45o is greater than the critical angle.
 10.a.i.
10.a.i.
 a.ii. Individual electrons in the metal atom absorb the energy of a single
photon, the energy of which is dependent on the frequency of the photon.
The photon energy can be calculated using the equation E = hf. Below
a certain frequency the energy absorbed by an electronin the metal, from
the photon, is below that required to escape from the metal atom, thus
the current in the circuit will be zero.
b.i. The threshold frequency will provide electrons with just enough
energy to overcome the work function of the metal and eject electrons
with no excess kinetic energy. Thus to estimate the work function from the
graph the line must be extrapolated until it cuts the x-axis of the
graph.
X-axis intercept = 6.7x1014Hz
This is the threshold frequency.
b.ii. The work function is calculated using:
Ework function = hfthreshold
Ework function = 6.63x10-34x6.6x1014
Ework function = 4.4x10-19J
This is closest to the work function of the metal calcium
11.a. Alpha particles have a positive charge. It was therefore concluded
that electrostatic repulsion from a like charge, of very large mass,
was required to produce a large angle deflection. However, as large
angle deflections were very rare, and most alpha particles were
undeviated from their original path, it led Rutherford to conclude
that most of the atom was empty space with the large positive mass
concentrated at the centre of the atom.
b.i. The total dose equivalent received is calculated using the equation:
H =QD.
Hgamma = QgammaDgamma
Hgamma = 1x200
Hgamma = 200mSv
Hneutrons = QneutronsDneutrons
Hneutrons = 3x100
Hneutrons = 300mSv
Htotal = Hgamma + Hneutrons
Htotal = 200 + 300
Htotal = 500mSv
b.ii.
a.ii. Individual electrons in the metal atom absorb the energy of a single
photon, the energy of which is dependent on the frequency of the photon.
The photon energy can be calculated using the equation E = hf. Below
a certain frequency the energy absorbed by an electronin the metal, from
the photon, is below that required to escape from the metal atom, thus
the current in the circuit will be zero.
b.i. The threshold frequency will provide electrons with just enough
energy to overcome the work function of the metal and eject electrons
with no excess kinetic energy. Thus to estimate the work function from the
graph the line must be extrapolated until it cuts the x-axis of the
graph.
X-axis intercept = 6.7x1014Hz
This is the threshold frequency.
b.ii. The work function is calculated using:
Ework function = hfthreshold
Ework function = 6.63x10-34x6.6x1014
Ework function = 4.4x10-19J
This is closest to the work function of the metal calcium
11.a. Alpha particles have a positive charge. It was therefore concluded
that electrostatic repulsion from a like charge, of very large mass,
was required to produce a large angle deflection. However, as large
angle deflections were very rare, and most alpha particles were
undeviated from their original path, it led Rutherford to conclude
that most of the atom was empty space with the large positive mass
concentrated at the centre of the atom.
b.i. The total dose equivalent received is calculated using the equation:
H =QD.
Hgamma = QgammaDgamma
Hgamma = 1x200
Hgamma = 200mSv
Hneutrons = QneutronsDneutrons
Hneutrons = 3x100
Hneutrons = 300mSv
Htotal = Hgamma + Hneutrons
Htotal = 200 + 300
Htotal = 500mSv
b.ii.
 Three half value thicknesses are required.
3t1/2 = 3x8 = 24mm
Three half value thicknesses are required.
3t1/2 = 3x8 = 24mm