
Solutions to SQA examination
1994 Higher Grade Physics
Paper II Solutions
Return to past paper index page.
1.a.i. At the maximum height the long jumpers vertical velocity(Vv) is 0m/s.
vv = 0m/s
Sv = 0.86m
a = -9.8m/s/s
uv = ?
To find u use : v2 = u2 + 2as
02 = u2 + 2x(-9.8)x0.86
u2 = 16.856(m/s)2
u = 4.1m/s
Note: The positive square root is taken because
the motion is in the upwards direction.
a.ii. The total time in the air for the vertical jump in part a.i. will be
the same as that for the actual jump if the vertical component of velocity
is the same.
The total displacement for the jump in part a.i. is 0m.
s = 0m
a = -9.8m/s/s
u = 4.1m/s
t = ?
To solve for t use: s = ut + 1/2(at2)
0 = ut + 1/2(at2)....divide by t
0 = u + (at)/2
t = -2u/a
t = (-2x4.1)/-9.8
t = 0.84s
vH = sH/t
vH = 7.8/0.84
vH = 9.3m/s
b. With a maximum height of less than 0.86m the time in the air would
be less than that 0.84s. This means that the horizontal distance
must be covered in a shorter time. This can only be achieved if
the horizontal velocity is greater than 9.3m/s.
2.a.i.
 a.ii. m = 500kg
g = 9.8N/kg
W = ?
W = mg
W = 500x9.8
W = 4900N
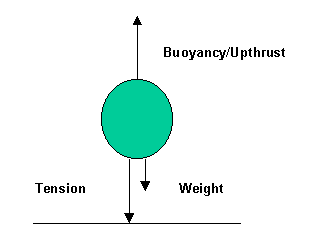
With no rope in position there is no tension force(T). This means
that the unbalance force causing the acceleration is the difference
between the buoyancy force(B) and the weight(W).
Fun = B - W
Fun = ma
ma = B - W
B = ma + W
B = 500x1.5 + 4900
B = 5650N
a.iii.Before the release the upward force must balance the downward forces.
B = W + T
T = B - W
T = 5650 - 4900
T = 750N
b.
a.ii. m = 500kg
g = 9.8N/kg
W = ?
W = mg
W = 500x9.8
W = 4900N
With no rope in position there is no tension force(T). This means
that the unbalance force causing the acceleration is the difference
between the buoyancy force(B) and the weight(W).
Fun = B - W
Fun = ma
ma = B - W
B = ma + W
B = 500x1.5 + 4900
B = 5650N
a.iii.Before the release the upward force must balance the downward forces.
B = W + T
T = B - W
T = 5650 - 4900
T = 750N
b.
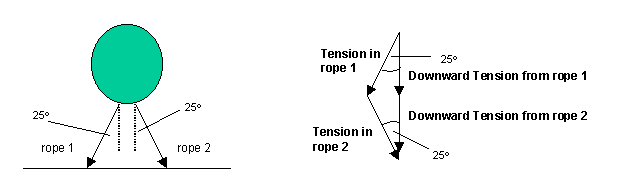 Each rope contributes half of the downward component of the tension.
Downward tension from rope 1 = 375N
Downward tension from rope 2 = 375N
To calculate the tension in each rope use trigonometry.
375/Trope 1 = cos25o
Trope 1 = 375/cos25o
Trope 1 = 413.8N
375/Trope 2 = cos25o
Trope 2 = 375/cos25o
Trope 2 = 413.8N
4.a.i. Use Boyle's law to solve this problem.
P1 = 1.76x105Pa
V1 = 750cm3
P2 = ?
V2 = 900cm3
P1V1 = P2V2
P2 = P1V1/V2
P2 = 1.76x105x750/900
P2 = 1.47x105Pa
a.ii. F = PA
F = 1.47x105x5x10-3
F = 735N
b. The gas inside the rocket exerts the forces shown in the diagram.
Each rope contributes half of the downward component of the tension.
Downward tension from rope 1 = 375N
Downward tension from rope 2 = 375N
To calculate the tension in each rope use trigonometry.
375/Trope 1 = cos25o
Trope 1 = 375/cos25o
Trope 1 = 413.8N
375/Trope 2 = cos25o
Trope 2 = 375/cos25o
Trope 2 = 413.8N
4.a.i. Use Boyle's law to solve this problem.
P1 = 1.76x105Pa
V1 = 750cm3
P2 = ?
V2 = 900cm3
P1V1 = P2V2
P2 = P1V1/V2
P2 = 1.76x105x750/900
P2 = 1.47x105Pa
a.ii. F = PA
F = 1.47x105x5x10-3
F = 735N
b. The gas inside the rocket exerts the forces shown in the diagram.
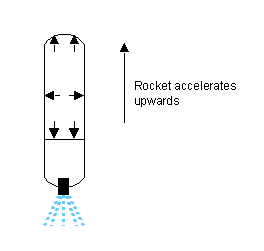
- The lateral forces cancel.
- The downward force accelerates the water out of the rocket.
- The upward force accelerates the rocket.
4.a. Ek = 1/2(mv2)
Collision with polyurethane block.
Ek = 1/2(0.5x0.332)
Ek = 0.027J
Collision with rubber band.
Ek = 1/2(0.5x0.432)
Ek = 0.046J
b. In elastic collisions kinetic energy is conserved.
In the collision with the metal spring the least amount of kinetic
energy is lost and is therefore the most like an elastic collision.
c. To propel the vehicle with the same initial speed the force providing
the impulse must be equal in each experiment. This could be achieved
if the impulse was provided by a stretched elastic band and ensuring
the band was pulled back by the same amount each time.
 d.i. F = (mv-mu)/tc
m = 0.5kg
tc = contact time = 0.4s
u = -0.55m/s
v = 0.35m/s
F = 0.5[0.35-(-0.55)]/0.4
F = 0.5x0.9/.4
F = 1.125N
d.ii. The vehicle accelerates to the right when in contact with the block.
This is because the direction of the force causing the acceleration
is towards the right and the acceleration must be in the same direction.
5.a.i. Vsupply = Vx + Vy
Vx = Vsupply - Vy
Vx = 10 - 6
Vx = 4V
Ix = Vx/Rx
Ix = 4/1200
Ix = 0.0033A
Ix = Iy = 0.0033A
Vy = IyRy
Ry = Vy/Iy
Ry = 6/0.0033
Ry = 1800W = 1.8kW
5.a.ii. The voltage across each resistor in a potential divider circuit
is proportional to the value of its resistance. When resistor Z
is connected in parallel with resistor Y a parallel network, with
a lower resistance than resistor Y alone, is created. The voltage across
this network, and each resistor in the network, is therefore less than
the voltage across Y alone.
5.a.iii.1/Rp = 1/RY + 1/RZ
1/Rp = 1/1.8 + 1/4.7
1/Rp = 0.5555 + 0.2128
1/Rp = 0.7683
Rp = 1.3kW
VRp = [Rp/(RX+Rp)]Vsupply
VRp = [1.3/(1.3+1.2)]10
VRp = 0.52x10
VRp = 5.2V
5.b.i. RA/RB = RC/RD
d.i. F = (mv-mu)/tc
m = 0.5kg
tc = contact time = 0.4s
u = -0.55m/s
v = 0.35m/s
F = 0.5[0.35-(-0.55)]/0.4
F = 0.5x0.9/.4
F = 1.125N
d.ii. The vehicle accelerates to the right when in contact with the block.
This is because the direction of the force causing the acceleration
is towards the right and the acceleration must be in the same direction.
5.a.i. Vsupply = Vx + Vy
Vx = Vsupply - Vy
Vx = 10 - 6
Vx = 4V
Ix = Vx/Rx
Ix = 4/1200
Ix = 0.0033A
Ix = Iy = 0.0033A
Vy = IyRy
Ry = Vy/Iy
Ry = 6/0.0033
Ry = 1800W = 1.8kW
5.a.ii. The voltage across each resistor in a potential divider circuit
is proportional to the value of its resistance. When resistor Z
is connected in parallel with resistor Y a parallel network, with
a lower resistance than resistor Y alone, is created. The voltage across
this network, and each resistor in the network, is therefore less than
the voltage across Y alone.
5.a.iii.1/Rp = 1/RY + 1/RZ
1/Rp = 1/1.8 + 1/4.7
1/Rp = 0.5555 + 0.2128
1/Rp = 0.7683
Rp = 1.3kW
VRp = [Rp/(RX+Rp)]Vsupply
VRp = [1.3/(1.3+1.2)]10
VRp = 0.52x10
VRp = 5.2V
5.b.i. RA/RB = RC/RD
b.ii.
| Resistance of A/W | Resistance of B/W | Voltmeter reading/mV |
| 120 | 120 | 0 |
| 121 | 120 | -21 |
| 121 | 121 | 0 |
| 121 | 122 | +21 |
| 121 | 119 | -42 |
The values in the table are worked out using the fact that the
voltage reading is proportional to the out of balance resistance.
6.a.i. Q = Ixt
Q = ?
I = 0.5A
t = 1h = 3600s
Q = 0.5x3600
Q = 1800C
6.a.ii. E = Pt
P = IV
=>E=ItV
E = 0.5x3600x1.2
E = 2160J
OR
E = QV (same answer)
b.i. The emf is the energy the cell supplies to each coulomb of charge
passing through it.
b.ii. The emf can be found by projecting the graph line back until it
cuts the voltage axis.
emf = 1.4V
The internal resistance is equal to the negative of the gradient
of the line given.
m = (y1-y2)/(x1-x2)
m = (1.0-0.6)/(1.0-2.0)
m = 0.4/-0.1
m = -4
r = 4W
To justify the above consider:
y = mx + c ...1
V = mI + c ...2
Vtpd= E - Ir ...3
Vtpd= -Ir + E ...4
From equation (3)
When I = 0A :Vtpd=emf
Comparing (2) and (4)
m = -r
7.a.i. The light from the window will result in the solar cell producing
a small voltage that is amplified to produce a non zero Vout.
a.ii. Vout/Vin = Rfeedback/R1
Vin = -Vout(R1/Rfeedback)
Vin = -(-1.75)(15/120)
Vin = 0.219V
b.i. The differential amplifier amplifies the difference between V1 and V2.
When V1 is adjusted to equal V2 there is no difference between
the input voltages and the output voltage will be zero.
b.ii. Vout = Rf/R1(V2-V1)
1.5 = 220/4.7(V2-0.219)
1.5 = 46.81(V2-0.219)
0.032 = V2-0.219
V2 = 0.251V
8.a. T = 4x5ms
T = 20ms
f = 1/T
f = 1/20x10-3
f = 50Hz
b.i. The value of resistor R2 was increased. This conclusion is drawn
because the rate at which the capacitor discharges has decreased.
b.ii. Q = CDV
DV = Vinitial-Vfinal
DV = 8V - 2V = 6V
Q = 2.2x10-6x6
Q = 1.32x10-5C
9.a.i. nplastic = sinqair/sinqplastic
nplastic = sin40o/sin30o
nplastic = 0.633/0.5
nplastic = 1.29
a.ii.
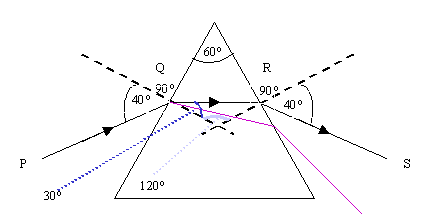 b.i. qcritical = sin-1(1/n)
qcritical = sin-1(1/1.8)
qcritical = sin-1(0.555)
qcritical = 33.7o
b.ii. nborate glass = sinqair/sinqborate glass
sinqborate glass = sinqair/nborate glass
sinqborate glass = sin40o/1.8
sinqborate glass = 0.0.643/1.8
sinqborate glass = 0.357
qborate glass = 20.9o
b.i. qcritical = sin-1(1/n)
qcritical = sin-1(1/1.8)
qcritical = sin-1(0.555)
qcritical = 33.7o
b.ii. nborate glass = sinqair/sinqborate glass
sinqborate glass = sinqair/nborate glass
sinqborate glass = sin40o/1.8
sinqborate glass = 0.0.643/1.8
sinqborate glass = 0.357
qborate glass = 20.9o
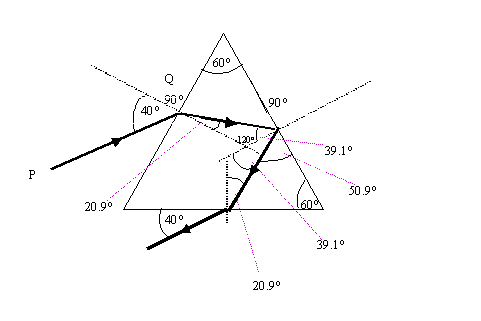 10.a.i. Electrons are moving from a high to low energy level within the atom.
A photon of light is emitted when this happens.
a.ii. lsodium yellow = 589nm
Ephoton = hf
Ephoton = hc/l
Ephoton = 6.63x10-34x3x108/589x10-9
Ephoton = 3.38x10-19J
The photon energy and the energy difference are equal.
Edifference = 3.38x10-19J
b.i. Photons emitted from the sodium lamp and passing through the flame containing
vaporised sodium will be absorbed by sodium electrons. This means that sodium
light passing through the flame will be reduced in intensity and produce a dark
shadow behind the flame.
b.ii. There is no energy gap in cadmium with the same energy as a photon emitted
from the sodium lamp. Therefore, no absorption will take place and there will
be no shadow region.
11.a. The activity(A), measured in becquerels(bq), is a measure of the number
of disintegrations(N) per second.
A = N/t
N = At
N = 300x106x60
N = 18x109
b. H/t = 16mSv/h (at a distance of 1m)
H = DQ
H/t = (D/t)xQ
16mSv/h = (50mGy/t)x1
t = 50mGy/16mSv/h
t = 3.125h
c.i.
10.a.i. Electrons are moving from a high to low energy level within the atom.
A photon of light is emitted when this happens.
a.ii. lsodium yellow = 589nm
Ephoton = hf
Ephoton = hc/l
Ephoton = 6.63x10-34x3x108/589x10-9
Ephoton = 3.38x10-19J
The photon energy and the energy difference are equal.
Edifference = 3.38x10-19J
b.i. Photons emitted from the sodium lamp and passing through the flame containing
vaporised sodium will be absorbed by sodium electrons. This means that sodium
light passing through the flame will be reduced in intensity and produce a dark
shadow behind the flame.
b.ii. There is no energy gap in cadmium with the same energy as a photon emitted
from the sodium lamp. Therefore, no absorption will take place and there will
be no shadow region.
11.a. The activity(A), measured in becquerels(bq), is a measure of the number
of disintegrations(N) per second.
A = N/t
N = At
N = 300x106x60
N = 18x109
b. H/t = 16mSv/h (at a distance of 1m)
H = DQ
H/t = (D/t)xQ
16mSv/h = (50mGy/t)x1
t = 50mGy/16mSv/h
t = 3.125h
c.i.

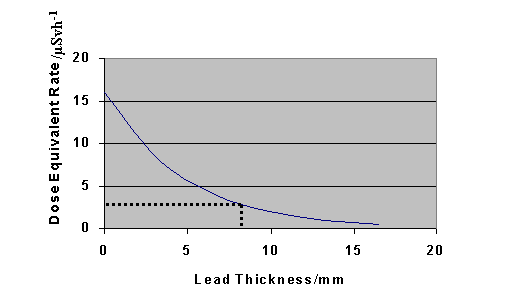 c.ii. The graph indicates that the required lead thickness is 8.8mm.
d. The polystyrene packaging increases the distance between the porters
and the source. As the intensity at a distance(d) from the source is
inversely proportional to the square of the distance the dose equivalent
rate for the porters will be less.
12.a. Mean(L) = Total/Number of readings
Mean(L) = (2.402+2.399+2.412+2.408+2.388+2.383+2.415)/7
Mean(L) = 16.807/7
Mean(L) = 2.401m
Random Error(L) = Range/Number of readings
Random Error(L) = (Max-Min)/N
Random Error(L) = (2.415-2.383)/7
Random Error(L) = 0.032/7
Random Error(L) = 0.005m
b. Percentage error in L = [Random Error(L)/Mean(L)]x100
Percentage error in L = [0.005/2.401]x100
Percentage error in L = 0.21%
Percentage error in x = [Random Error(x)/Mean(x)]x100
Percentage error in x = [1/91]x100
Percentage error in x = 1.1%
The measurement with the largest percentage error is x.
c. l = dsinq
l = dx/L
l = 1.693x10-591x10-3/2.401
l = 641.66nm
The percentage error in l can be taken to
be equal to the percentage error in x, as this is the largest individual
error.
1.1% of 641.66nm = (1.1/100)x641.66 = 7.06nm
l = (641.66 +- 7.06)nm
d. Increasing the distance between the grating
and the screen reduces the percentage error
of L and, more significantly, x.
c.ii. The graph indicates that the required lead thickness is 8.8mm.
d. The polystyrene packaging increases the distance between the porters
and the source. As the intensity at a distance(d) from the source is
inversely proportional to the square of the distance the dose equivalent
rate for the porters will be less.
12.a. Mean(L) = Total/Number of readings
Mean(L) = (2.402+2.399+2.412+2.408+2.388+2.383+2.415)/7
Mean(L) = 16.807/7
Mean(L) = 2.401m
Random Error(L) = Range/Number of readings
Random Error(L) = (Max-Min)/N
Random Error(L) = (2.415-2.383)/7
Random Error(L) = 0.032/7
Random Error(L) = 0.005m
b. Percentage error in L = [Random Error(L)/Mean(L)]x100
Percentage error in L = [0.005/2.401]x100
Percentage error in L = 0.21%
Percentage error in x = [Random Error(x)/Mean(x)]x100
Percentage error in x = [1/91]x100
Percentage error in x = 1.1%
The measurement with the largest percentage error is x.
c. l = dsinq
l = dx/L
l = 1.693x10-591x10-3/2.401
l = 641.66nm
The percentage error in l can be taken to
be equal to the percentage error in x, as this is the largest individual
error.
1.1% of 641.66nm = (1.1/100)x641.66 = 7.06nm
l = (641.66 +- 7.06)nm
d. Increasing the distance between the grating
and the screen reduces the percentage error
of L and, more significantly, x.
END OF QUESTION PAPER
Return to past paper index page.


a.ii. m = 500kg g = 9.8N/kg W = ? W = mg W = 500x9.8 W = 4900N With no rope in position there is no tension force(T). This means that the unbalance force causing the acceleration is the difference between the buoyancy force(B) and the weight(W). Fun = B - W Fun = ma ma = B - W B = ma + W B = 500x1.5 + 4900 B = 5650N a.iii.Before the release the upward force must balance the downward forces. B = W + T T = B - W T = 5650 - 4900 T = 750N b.
Each rope contributes half of the downward component of the tension. Downward tension from rope 1 = 375N Downward tension from rope 2 = 375N To calculate the tension in each rope use trigonometry. 375/Trope 1 = cos25o Trope 1 = 375/cos25o Trope 1 = 413.8N 375/Trope 2 = cos25o Trope 2 = 375/cos25o Trope 2 = 413.8N 4.a.i. Use Boyle's law to solve this problem. P1 = 1.76x105Pa V1 = 750cm3 P2 = ? V2 = 900cm3 P1V1 = P2V2 P2 = P1V1/V2 P2 = 1.76x105x750/900 P2 = 1.47x105Pa a.ii. F = PA F = 1.47x105x5x10-3 F = 735N b. The gas inside the rocket exerts the forces shown in the diagram.

d.i. F = (mv-mu)/tc m = 0.5kg tc = contact time = 0.4s u = -0.55m/s v = 0.35m/s F = 0.5[0.35-(-0.55)]/0.4 F = 0.5x0.9/.4 F = 1.125N d.ii. The vehicle accelerates to the right when in contact with the block. This is because the direction of the force causing the acceleration is towards the right and the acceleration must be in the same direction. 5.a.i. Vsupply = Vx + Vy Vx = Vsupply - Vy Vx = 10 - 6 Vx = 4V Ix = Vx/Rx Ix = 4/1200 Ix = 0.0033A Ix = Iy = 0.0033A Vy = IyRy Ry = Vy/Iy Ry = 6/0.0033 Ry = 1800W = 1.8kW 5.a.ii. The voltage across each resistor in a potential divider circuit is proportional to the value of its resistance. When resistor Z is connected in parallel with resistor Y a parallel network, with a lower resistance than resistor Y alone, is created. The voltage across this network, and each resistor in the network, is therefore less than the voltage across Y alone. 5.a.iii.1/Rp = 1/RY + 1/RZ 1/Rp = 1/1.8 + 1/4.7 1/Rp = 0.5555 + 0.2128 1/Rp = 0.7683 Rp = 1.3kW VRp = [Rp/(RX+Rp)]Vsupply VRp = [1.3/(1.3+1.2)]10 VRp = 0.52x10 VRp = 5.2V 5.b.i. RA/RB = RC/RD
b.i. qcritical = sin-1(1/n) qcritical = sin-1(1/1.8) qcritical = sin-1(0.555) qcritical = 33.7o b.ii. nborate glass = sinqair/sinqborate glass sinqborate glass = sinqair/nborate glass sinqborate glass = sin40o/1.8 sinqborate glass = 0.0.643/1.8 sinqborate glass = 0.357 qborate glass = 20.9o
10.a.i. Electrons are moving from a high to low energy level within the atom. A photon of light is emitted when this happens. a.ii. lsodium yellow = 589nm Ephoton = hf Ephoton = hc/l Ephoton = 6.63x10-34x3x108/589x10-9 Ephoton = 3.38x10-19J The photon energy and the energy difference are equal. Edifference = 3.38x10-19J b.i. Photons emitted from the sodium lamp and passing through the flame containing vaporised sodium will be absorbed by sodium electrons. This means that sodium light passing through the flame will be reduced in intensity and produce a dark shadow behind the flame. b.ii. There is no energy gap in cadmium with the same energy as a photon emitted from the sodium lamp. Therefore, no absorption will take place and there will be no shadow region. 11.a. The activity(A), measured in becquerels(bq), is a measure of the number of disintegrations(N) per second. A = N/t N = At N = 300x106x60 N = 18x109 b. H/t = 16mSv/h (at a distance of 1m) H = DQ H/t = (D/t)xQ 16mSv/h = (50mGy/t)x1 t = 50mGy/16mSv/h t = 3.125h c.i.

c.ii. The graph indicates that the required lead thickness is 8.8mm. d. The polystyrene packaging increases the distance between the porters and the source. As the intensity at a distance(d) from the source is inversely proportional to the square of the distance the dose equivalent rate for the porters will be less. 12.a. Mean(L) = Total/Number of readings Mean(L) = (2.402+2.399+2.412+2.408+2.388+2.383+2.415)/7 Mean(L) = 16.807/7 Mean(L) = 2.401m Random Error(L) = Range/Number of readings Random Error(L) = (Max-Min)/N Random Error(L) = (2.415-2.383)/7 Random Error(L) = 0.032/7 Random Error(L) = 0.005m b. Percentage error in L = [Random Error(L)/Mean(L)]x100 Percentage error in L = [0.005/2.401]x100 Percentage error in L = 0.21% Percentage error in x = [Random Error(x)/Mean(x)]x100 Percentage error in x = [1/91]x100 Percentage error in x = 1.1% The measurement with the largest percentage error is x. c. l = dsinq l = dx/L l = 1.693x10-591x10-3/2.401 l = 641.66nm The percentage error in l can be taken to be equal to the percentage error in x, as this is the largest individual error. 1.1% of 641.66nm = (1.1/100)x641.66 = 7.06nm l = (641.66 +- 7.06)nm d. Increasing the distance between the grating and the screen reduces the percentage error of L and, more significantly, x.