
Solutions to SQA examination
1993 Higher Grade Physics
Paper II Solutions
Return to past paper index page.
1.a. The ball is in free fall for the first 0.5s.
u = 0m/s
v = -4.5m/s
t = 0.5s
a = ?
a = (v-u)/t
a = (-4.5-0)/0.5
a = -9.0m/s/s
b. DEk = Ekafter-Ekbefore
DEk = 1/2(mv2-mu2)
2DEk = m(v2-u2)
2DEk/(v2-u2) = m
m = 2DEk/(v2-u2)
m = 2x-1.7/(42-[-4.52])
m = -3.4/(16-20.25)
m = 0.8kg
c. DP = mv-mu
DP = m(v-u)
DP = 0.8(4-[-4.5])
DP = 6.8kgm/s
d. The time that the ball is in contact with the ground(tc) is 0.5s.
F = DP/tc
F = 6.8/0.5
F = 13.6N
2.a.
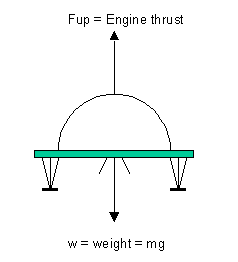 w = ?
m = 15000
g = 1.6N/kg
w = mg
w = 15000x1.6
w = 24000N
The upward force(Fup) is equal in magnitude to the weight
and acts in the opposite direction. There is no unbalanced force
which means the craft must be moving at a constant speed and be moving
in a straight line.
b.i. Funbalanced = Fup - w
Funbalanced = 25500 - 24000
Funbalanced = 1500N
a = Funbalanced/m
a = 1500/15000
a = 0.1m/s/s upwards
This means that the craft has an upward deceleration of -0.1m/s/s.
b.ii. a = 0.1m/s/s
t = 18s
u = -2.0m/s
v = ?
v = u + at
v = -2.0 + 0.1x18
v = -0.2m/s
b.iii.v2 = u2 + 2as
s = (v2-u2)/2a
s = ([-0.2]2-[-2]2)/2x0.1
s = (0.04-4)/0.2
s = -3.96/0.2
s = -19.8m
This displacement is equal to that which the craft has descended from.
This means the craft must have been 19.8m above the surface of the moon
to start with.
3.a. The law of conservation of linear momentum states that :
Pbefore = Pafter
b.i. Before collision
Pbefore = mAuA + mBuB
Pbefore = 1400xuA + 1000x8
Pbefore = 1400uA + 8000
After collision
Pafter = mAvA + mBvB
vA=vB=v
Pafter = (mA + mB)v
Pafter = (1400 + 1000)15
Pafter = 36000kgm/s
Equate: Pbefore and Pafter
1400uA + 8000 = 36000kgm/s
1400uA = (36000-8000)/1400
uA = 20m/s
b.ii. Consider the instant after the collision to be the starting point
for this calculation.
u = 15m/s
v = 0m/s
s = 20m
a = ?
v2 = u2 + 2as
a = (v2-u2)/2s
a = (02-152)/2x20
a = -225/40
a = -5.625m/s/s
Ffriction = Fun
Fun = ma
Fun = 2400x-5.625
Fun = -13,500N The negative sign indicates that the force
acts to the LHS.
OR
The kinetic energy lost by the car is equal to the work done by
the frictional force over the 20m stopping distance.
Eklost = Ework
Eklost = Ekbefore - Ekafter
Eklost = (mv2 - mu2)/2
Eklost = m(v2 - u2)/2
Eklost = 2400(152 - 02)/2
Eklost = 27000J
Ework = Fd
F = Ework/d
F = 27000/20
F = 13500N
b.iii.Most of the kinetic energy will be converted into heat energy.
4.a. P1 = 400kPa
V1 = 1000cm3
P2 = 250kPa
V2 = ?
P1V1 = P2V2
V2 = P1V1/P2
V2 = 400x1000/250
V2 = 1600cm3
b. The pressure increases.
The volume remains constant.
The temperature increases.
c. The starting pressure is that indicated by point B on the graph
and the final pressure is that indicated by point C. Over this
period the volume is constant.
T1 = 300K
P1 = 200kPa
T2 = ?
P2 = 500kPa
P1/T1 = P2/T2
T2 = P2(T1/P1)
T2 = 500(300/200)
T2 = 750K
5.a.i. Q = CV
C = Q/V
C = 24x10-6/1.5
C = 16x10-6F
C = 16mF
a.ii. Mean = total/N
Mean(C) = (16+18+20+16+15)/5
Mean(C) = 17mF
Random error = (max-min)/N
Random error(C) = (20-15)/5
Random error(C) = +-1mF
C = (17+-1)mF
a.iii.Measure the voltage across the capacitor directly by connecting
the voltmeter across it. Additionally, to prevent leakage through
the voltmeter it would be better to use an oscilloscope for this
purpose.
b. The effective resistance of the capacitor in the circuit decreases
as the frequency of the supply increase. As the resistance decreases
the current in the circuit increases and the lamp glows more brightly.
6.a. The electromotive force is the energy supplied by the power supply
to each coulomb of charge.
b.i. P = I2R
I2 = P/R
I = (P/R)1/2
I = (8.0/0.32)1/2
I = 251/2
I = 5A
b.ii. V = IR
V = 5x0.32
V = 1.6V
b.iii.Vr = emf - Vheater
Vr = 2.0 - 1.6
Vr = 0.4V
Vr = Ir
r = Vr/I
r = 0.4/5
r = 0.08W
c. Two heaters in parallel will reduce the resistance of the circuit.
The current in the heater elements will increase which has the
effect of increasing the rate at which the water is heated.
The resistance of the two heaters in parallel can be calculated as
shown below:
Rp = Rheater/2
Rp = 0.32/2
Rp = 0.16W
Rtotal = Rp + r
Rtotal = 0.16 + 0.08
Rtotal = 0.24W
I = emf/Rtotal
I = 2.0/0.24
I = 8.33A
Vr = Ir
Vr = 8.33x0.08
Vr = 0.67V
Vheater = emf - Vr
Vheater = 2.0 - 0.67
Vheater = 1.33V
This is the voltage across each heater element.
Iheater = Vheater/Rheater
Iheater = 1.33/0.32
Iheater = 4.16A
The power developed in each heater can be calculated using:
P = I2R
P = 4.162x0.32
P = 5.5W
The two heating elements develop a total power of 11W.
This means that the water is heated about 1.4 times faster.
7.a.i. The amplifier is working in inverting mode.
a.ii. Gain = -Rfeedback/R1
Gain = -1x106/2x103
Gain = 500
a.iii.
w = ?
m = 15000
g = 1.6N/kg
w = mg
w = 15000x1.6
w = 24000N
The upward force(Fup) is equal in magnitude to the weight
and acts in the opposite direction. There is no unbalanced force
which means the craft must be moving at a constant speed and be moving
in a straight line.
b.i. Funbalanced = Fup - w
Funbalanced = 25500 - 24000
Funbalanced = 1500N
a = Funbalanced/m
a = 1500/15000
a = 0.1m/s/s upwards
This means that the craft has an upward deceleration of -0.1m/s/s.
b.ii. a = 0.1m/s/s
t = 18s
u = -2.0m/s
v = ?
v = u + at
v = -2.0 + 0.1x18
v = -0.2m/s
b.iii.v2 = u2 + 2as
s = (v2-u2)/2a
s = ([-0.2]2-[-2]2)/2x0.1
s = (0.04-4)/0.2
s = -3.96/0.2
s = -19.8m
This displacement is equal to that which the craft has descended from.
This means the craft must have been 19.8m above the surface of the moon
to start with.
3.a. The law of conservation of linear momentum states that :
Pbefore = Pafter
b.i. Before collision
Pbefore = mAuA + mBuB
Pbefore = 1400xuA + 1000x8
Pbefore = 1400uA + 8000
After collision
Pafter = mAvA + mBvB
vA=vB=v
Pafter = (mA + mB)v
Pafter = (1400 + 1000)15
Pafter = 36000kgm/s
Equate: Pbefore and Pafter
1400uA + 8000 = 36000kgm/s
1400uA = (36000-8000)/1400
uA = 20m/s
b.ii. Consider the instant after the collision to be the starting point
for this calculation.
u = 15m/s
v = 0m/s
s = 20m
a = ?
v2 = u2 + 2as
a = (v2-u2)/2s
a = (02-152)/2x20
a = -225/40
a = -5.625m/s/s
Ffriction = Fun
Fun = ma
Fun = 2400x-5.625
Fun = -13,500N The negative sign indicates that the force
acts to the LHS.
OR
The kinetic energy lost by the car is equal to the work done by
the frictional force over the 20m stopping distance.
Eklost = Ework
Eklost = Ekbefore - Ekafter
Eklost = (mv2 - mu2)/2
Eklost = m(v2 - u2)/2
Eklost = 2400(152 - 02)/2
Eklost = 27000J
Ework = Fd
F = Ework/d
F = 27000/20
F = 13500N
b.iii.Most of the kinetic energy will be converted into heat energy.
4.a. P1 = 400kPa
V1 = 1000cm3
P2 = 250kPa
V2 = ?
P1V1 = P2V2
V2 = P1V1/P2
V2 = 400x1000/250
V2 = 1600cm3
b. The pressure increases.
The volume remains constant.
The temperature increases.
c. The starting pressure is that indicated by point B on the graph
and the final pressure is that indicated by point C. Over this
period the volume is constant.
T1 = 300K
P1 = 200kPa
T2 = ?
P2 = 500kPa
P1/T1 = P2/T2
T2 = P2(T1/P1)
T2 = 500(300/200)
T2 = 750K
5.a.i. Q = CV
C = Q/V
C = 24x10-6/1.5
C = 16x10-6F
C = 16mF
a.ii. Mean = total/N
Mean(C) = (16+18+20+16+15)/5
Mean(C) = 17mF
Random error = (max-min)/N
Random error(C) = (20-15)/5
Random error(C) = +-1mF
C = (17+-1)mF
a.iii.Measure the voltage across the capacitor directly by connecting
the voltmeter across it. Additionally, to prevent leakage through
the voltmeter it would be better to use an oscilloscope for this
purpose.
b. The effective resistance of the capacitor in the circuit decreases
as the frequency of the supply increase. As the resistance decreases
the current in the circuit increases and the lamp glows more brightly.
6.a. The electromotive force is the energy supplied by the power supply
to each coulomb of charge.
b.i. P = I2R
I2 = P/R
I = (P/R)1/2
I = (8.0/0.32)1/2
I = 251/2
I = 5A
b.ii. V = IR
V = 5x0.32
V = 1.6V
b.iii.Vr = emf - Vheater
Vr = 2.0 - 1.6
Vr = 0.4V
Vr = Ir
r = Vr/I
r = 0.4/5
r = 0.08W
c. Two heaters in parallel will reduce the resistance of the circuit.
The current in the heater elements will increase which has the
effect of increasing the rate at which the water is heated.
The resistance of the two heaters in parallel can be calculated as
shown below:
Rp = Rheater/2
Rp = 0.32/2
Rp = 0.16W
Rtotal = Rp + r
Rtotal = 0.16 + 0.08
Rtotal = 0.24W
I = emf/Rtotal
I = 2.0/0.24
I = 8.33A
Vr = Ir
Vr = 8.33x0.08
Vr = 0.67V
Vheater = emf - Vr
Vheater = 2.0 - 0.67
Vheater = 1.33V
This is the voltage across each heater element.
Iheater = Vheater/Rheater
Iheater = 1.33/0.32
Iheater = 4.16A
The power developed in each heater can be calculated using:
P = I2R
P = 4.162x0.32
P = 5.5W
The two heating elements develop a total power of 11W.
This means that the water is heated about 1.4 times faster.
7.a.i. The amplifier is working in inverting mode.
a.ii. Gain = -Rfeedback/R1
Gain = -1x106/2x103
Gain = 500
a.iii.
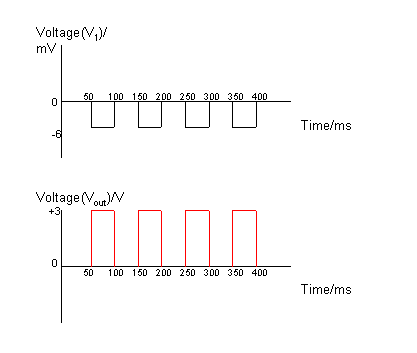 a.iv. The LED will pulse ON/OFF.
The LED will be on when Vout is positive.
The LED will be off when Vout is zero.
b.i. The op-amp is working in differential mode.
The gain equation for the op-amp in this mode is:
Vout = (Rf/R1)(V2-V1)
b.ii. Use the equation in b.ii. to calculate Vout. Take the
voltages V1 and V2 from the graphs given.
a.iv. The LED will pulse ON/OFF.
The LED will be on when Vout is positive.
The LED will be off when Vout is zero.
b.i. The op-amp is working in differential mode.
The gain equation for the op-amp in this mode is:
Vout = (Rf/R1)(V2-V1)
b.ii. Use the equation in b.ii. to calculate Vout. Take the
voltages V1 and V2 from the graphs given.
| Time interval/ms |
V2/mV |
V1/mV |
Vout/V |
| 0-50 |
0 |
0 |
0 |
| 50-100 |
-6 |
-6 |
0 |
| 100-150 |
+6 |
0 |
+3 |
| 150-200 |
0 |
-6 |
+3 |
| 200-250 |
0 |
0 |
0 |
| 250-300 |
-6 |
-6 |
0 |
| 300-350 |
+6 |
0 |
+3 |
| 350-400 |
0 |
-6 |
+3 |
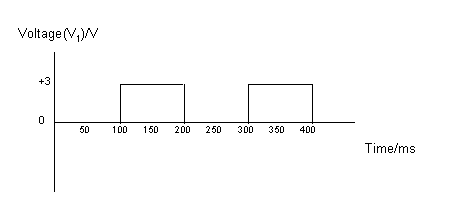 8.a. A ray of sunlight is made up of many different wavelengths that
is perceived as white light. However, each individual wavelength
represents a particular colour of light.
The diffraction grating diffracts the different wavelengths in
sunlight by different amounts: the longer wavelengths being
diffracted the most and the shorter wavelengths the least.
At position X on the screen the short wavelength violet light
has interfered constructively to produce a band of violet light.
At position Y on the screen the long wavelength red light
has interfered constructively to produce a band of red light.
Between X and Y the other colours of the visible spectrum produce
bands of indigo, blue, green, yellow and orange light.
b.i. dsinq = nl
d = 1/N = 1/6x105 = 1.667x10-6m
q = ?
n = 1
l = 410nm = 410x10-9m
sinq = nl/d
sinq = 1x410x10-9/1.667x10-6
sinq = 0.246
q = sin-10.246
q = 14.2o
b.ii. d = 1.667x10-6m
q = 14.2o + 9o = 23.2o
n = 1
l = ?
l = dsinq/n
l = 1.667x10-6sin(23.2o)/1
l = 656.7x10-9m = 656.7nm
c. The diffraction grating will produce many spectra symmetrical about the
q = 0o line.
The prism produces one spectrum by refraction.
The relative positions of each colour of light produced
by refraction will be the reverse of that produced by the
diffraction grating, as blue light is refracted more than
red light.
9.a. Monochromatic means the laser light has a single wavelength/frequency.
Coherent means the waves are in phase/step.
b.i. DE = hf where DE = E2-E2
f = E2-E2/h
f = -4.67x10-20-(-6.55x10-20)/6.63x10-34
f = 452.5nm
b.ii. The wavelength of the emitted radiation corresponds to the blue end of
the spectrum.
c. The beam is intense because the energy is spread over a small area and
a large number of photons per second are emitted from the laser.
10.a. Light incident on the pn-junction photodiode will increase the number
of electron hole pairs and consequently increase the conductivity of
the diode.
b. The diode is operating in photoconductive mode.
c. I1d12 = I2d22
I2 = I1d12/d22
I2 = 3.0x12/0.752
I2 = 5.33mA
11.a.i.
8.a. A ray of sunlight is made up of many different wavelengths that
is perceived as white light. However, each individual wavelength
represents a particular colour of light.
The diffraction grating diffracts the different wavelengths in
sunlight by different amounts: the longer wavelengths being
diffracted the most and the shorter wavelengths the least.
At position X on the screen the short wavelength violet light
has interfered constructively to produce a band of violet light.
At position Y on the screen the long wavelength red light
has interfered constructively to produce a band of red light.
Between X and Y the other colours of the visible spectrum produce
bands of indigo, blue, green, yellow and orange light.
b.i. dsinq = nl
d = 1/N = 1/6x105 = 1.667x10-6m
q = ?
n = 1
l = 410nm = 410x10-9m
sinq = nl/d
sinq = 1x410x10-9/1.667x10-6
sinq = 0.246
q = sin-10.246
q = 14.2o
b.ii. d = 1.667x10-6m
q = 14.2o + 9o = 23.2o
n = 1
l = ?
l = dsinq/n
l = 1.667x10-6sin(23.2o)/1
l = 656.7x10-9m = 656.7nm
c. The diffraction grating will produce many spectra symmetrical about the
q = 0o line.
The prism produces one spectrum by refraction.
The relative positions of each colour of light produced
by refraction will be the reverse of that produced by the
diffraction grating, as blue light is refracted more than
red light.
9.a. Monochromatic means the laser light has a single wavelength/frequency.
Coherent means the waves are in phase/step.
b.i. DE = hf where DE = E2-E2
f = E2-E2/h
f = -4.67x10-20-(-6.55x10-20)/6.63x10-34
f = 452.5nm
b.ii. The wavelength of the emitted radiation corresponds to the blue end of
the spectrum.
c. The beam is intense because the energy is spread over a small area and
a large number of photons per second are emitted from the laser.
10.a. Light incident on the pn-junction photodiode will increase the number
of electron hole pairs and consequently increase the conductivity of
the diode.
b. The diode is operating in photoconductive mode.
c. I1d12 = I2d22
I2 = I1d12/d22
I2 = 3.0x12/0.752
I2 = 5.33mA
11.a.i.
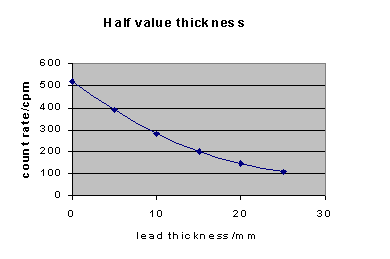 a.ii. Take the background count to be 20cpm.
Add this to the corrected count rate and plot as shown below.
a.ii. Take the background count to be 20cpm.
Add this to the corrected count rate and plot as shown below.
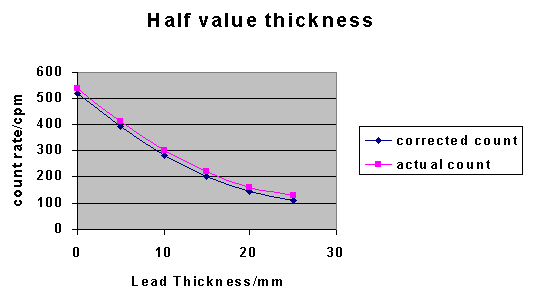 b. Time/years Corrected Count Rate/cpm
0 520
5.25 260
11.5 130
16.75 65
21 32.5
After 21 years the count rate is 32.5cpm.
b. Time/years Corrected Count Rate/cpm
0 520
5.25 260
11.5 130
16.75 65
21 32.5
After 21 years the count rate is 32.5cpm.
END OF QUESTION PAPER
Return to past paper index page.


w = ? m = 15000 g = 1.6N/kg w = mg w = 15000x1.6 w = 24000N The upward force(Fup) is equal in magnitude to the weight and acts in the opposite direction. There is no unbalanced force which means the craft must be moving at a constant speed and be moving in a straight line. b.i. Funbalanced = Fup - w Funbalanced = 25500 - 24000 Funbalanced = 1500N a = Funbalanced/m a = 1500/15000 a = 0.1m/s/s upwards This means that the craft has an upward deceleration of -0.1m/s/s. b.ii. a = 0.1m/s/s t = 18s u = -2.0m/s v = ? v = u + at v = -2.0 + 0.1x18 v = -0.2m/s b.iii.v2 = u2 + 2as s = (v2-u2)/2a s = ([-0.2]2-[-2]2)/2x0.1 s = (0.04-4)/0.2 s = -3.96/0.2 s = -19.8m This displacement is equal to that which the craft has descended from. This means the craft must have been 19.8m above the surface of the moon to start with. 3.a. The law of conservation of linear momentum states that : Pbefore = Pafter b.i. Before collision Pbefore = mAuA + mBuB Pbefore = 1400xuA + 1000x8 Pbefore = 1400uA + 8000 After collision Pafter = mAvA + mBvB vA=vB=v Pafter = (mA + mB)v Pafter = (1400 + 1000)15 Pafter = 36000kgm/s Equate: Pbefore and Pafter 1400uA + 8000 = 36000kgm/s 1400uA = (36000-8000)/1400 uA = 20m/s b.ii. Consider the instant after the collision to be the starting point for this calculation. u = 15m/s v = 0m/s s = 20m a = ? v2 = u2 + 2as a = (v2-u2)/2s a = (02-152)/2x20 a = -225/40 a = -5.625m/s/s Ffriction = Fun Fun = ma Fun = 2400x-5.625 Fun = -13,500N The negative sign indicates that the force acts to the LHS. OR The kinetic energy lost by the car is equal to the work done by the frictional force over the 20m stopping distance. Eklost = Ework Eklost = Ekbefore - Ekafter Eklost = (mv2 - mu2)/2 Eklost = m(v2 - u2)/2 Eklost = 2400(152 - 02)/2 Eklost = 27000J Ework = Fd F = Ework/d F = 27000/20 F = 13500N b.iii.Most of the kinetic energy will be converted into heat energy. 4.a. P1 = 400kPa V1 = 1000cm3 P2 = 250kPa V2 = ? P1V1 = P2V2 V2 = P1V1/P2 V2 = 400x1000/250 V2 = 1600cm3 b. The pressure increases. The volume remains constant. The temperature increases. c. The starting pressure is that indicated by point B on the graph and the final pressure is that indicated by point C. Over this period the volume is constant. T1 = 300K P1 = 200kPa T2 = ? P2 = 500kPa P1/T1 = P2/T2 T2 = P2(T1/P1) T2 = 500(300/200) T2 = 750K 5.a.i. Q = CV C = Q/V C = 24x10-6/1.5 C = 16x10-6F C = 16mF a.ii. Mean = total/N Mean(C) = (16+18+20+16+15)/5 Mean(C) = 17mF Random error = (max-min)/N Random error(C) = (20-15)/5 Random error(C) = +-1mF C = (17+-1)mF a.iii.Measure the voltage across the capacitor directly by connecting the voltmeter across it. Additionally, to prevent leakage through the voltmeter it would be better to use an oscilloscope for this purpose. b. The effective resistance of the capacitor in the circuit decreases as the frequency of the supply increase. As the resistance decreases the current in the circuit increases and the lamp glows more brightly. 6.a. The electromotive force is the energy supplied by the power supply to each coulomb of charge. b.i. P = I2R I2 = P/R I = (P/R)1/2 I = (8.0/0.32)1/2 I = 251/2 I = 5A b.ii. V = IR V = 5x0.32 V = 1.6V b.iii.Vr = emf - Vheater Vr = 2.0 - 1.6 Vr = 0.4V Vr = Ir r = Vr/I r = 0.4/5 r = 0.08W c. Two heaters in parallel will reduce the resistance of the circuit. The current in the heater elements will increase which has the effect of increasing the rate at which the water is heated. The resistance of the two heaters in parallel can be calculated as shown below: Rp = Rheater/2 Rp = 0.32/2 Rp = 0.16W Rtotal = Rp + r Rtotal = 0.16 + 0.08 Rtotal = 0.24W I = emf/Rtotal I = 2.0/0.24 I = 8.33A Vr = Ir Vr = 8.33x0.08 Vr = 0.67V Vheater = emf - Vr Vheater = 2.0 - 0.67 Vheater = 1.33V This is the voltage across each heater element. Iheater = Vheater/Rheater Iheater = 1.33/0.32 Iheater = 4.16A The power developed in each heater can be calculated using: P = I2R P = 4.162x0.32 P = 5.5W The two heating elements develop a total power of 11W. This means that the water is heated about 1.4 times faster. 7.a.i. The amplifier is working in inverting mode. a.ii. Gain = -Rfeedback/R1 Gain = -1x106/2x103 Gain = 500 a.iii.
a.iv. The LED will pulse ON/OFF. The LED will be on when Vout is positive. The LED will be off when Vout is zero. b.i. The op-amp is working in differential mode. The gain equation for the op-amp in this mode is: Vout = (Rf/R1)(V2-V1) b.ii. Use the equation in b.ii. to calculate Vout. Take the voltages V1 and V2 from the graphs given.
8.a. A ray of sunlight is made up of many different wavelengths that is perceived as white light. However, each individual wavelength represents a particular colour of light. The diffraction grating diffracts the different wavelengths in sunlight by different amounts: the longer wavelengths being diffracted the most and the shorter wavelengths the least. At position X on the screen the short wavelength violet light has interfered constructively to produce a band of violet light. At position Y on the screen the long wavelength red light has interfered constructively to produce a band of red light. Between X and Y the other colours of the visible spectrum produce bands of indigo, blue, green, yellow and orange light. b.i. dsinq = nl d = 1/N = 1/6x105 = 1.667x10-6m q = ? n = 1 l = 410nm = 410x10-9m sinq = nl/d sinq = 1x410x10-9/1.667x10-6 sinq = 0.246 q = sin-10.246 q = 14.2o b.ii. d = 1.667x10-6m q = 14.2o + 9o = 23.2o n = 1 l = ? l = dsinq/n l = 1.667x10-6sin(23.2o)/1 l = 656.7x10-9m = 656.7nm c. The diffraction grating will produce many spectra symmetrical about the q = 0o line. The prism produces one spectrum by refraction. The relative positions of each colour of light produced by refraction will be the reverse of that produced by the diffraction grating, as blue light is refracted more than red light. 9.a. Monochromatic means the laser light has a single wavelength/frequency. Coherent means the waves are in phase/step. b.i. DE = hf where DE = E2-E2 f = E2-E2/h f = -4.67x10-20-(-6.55x10-20)/6.63x10-34 f = 452.5nm b.ii. The wavelength of the emitted radiation corresponds to the blue end of the spectrum. c. The beam is intense because the energy is spread over a small area and a large number of photons per second are emitted from the laser. 10.a. Light incident on the pn-junction photodiode will increase the number of electron hole pairs and consequently increase the conductivity of the diode. b. The diode is operating in photoconductive mode. c. I1d12 = I2d22 I2 = I1d12/d22 I2 = 3.0x12/0.752 I2 = 5.33mA 11.a.i.
a.ii. Take the background count to be 20cpm. Add this to the corrected count rate and plot as shown below.
b. Time/years Corrected Count Rate/cpm 0 520 5.25 260 11.5 130 16.75 65 21 32.5 After 21 years the count rate is 32.5cpm.