
Solutions to SQA examination
1992 Higher Grade Physics
Paper II Solutions
Return to past paper index page.
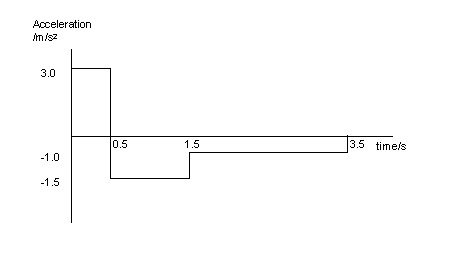
1.a. From 0s up to 1.5s(point B) the trolley is moving away from the sensor.
At 1.5s the trolley stops, changes direction, and moves back towards the
sensor for the next 2s.
This means the trolley is at its greatest distance from the trolley after 1.5s.
b. From OA From AB From BC
u = 0m/s u = 1.5m/s u = 0m/s
v = 1.5m/s v = 0m/s v = -1m/s
t = 0.5s t = 1s t = 2s
a = ? a = ? a = ?
a = (v-u)/t a = (v-u)/t a = (v-u)/t
a = (1.5-0)/0.5 a = (0-1.5)/1 a = (-1.0-0)/1
a0A = 3m/s/s aAB = -1.5m/s/s aBC = -1m/s/s
 c.
c.
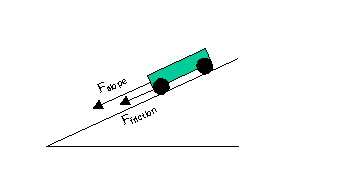 Fslope = component of gravitational force acting down the slope.
d. When moving up the slope: both Fslope and Ffriction are acting in
the same direction. This means that the unbalanced force causing
the acceleration between A and B is the sum of these two forces.
Funbalanced = Fslope + Ffriction
When moving down the slope: Ffriction acts up the slope, in the
opposite direction to Fslope. This means that the unbalanced force
causing the acceleration between B and C is the difference between
these two forces.
Funbalanced = Fslope - Ffriction
The acceleration is therefore greater when the trolley is moving up the slope.
2.a.i. Step 1 : Calculate the energy available from 0.7kg of fuel.
Eincrease = mass of fuel x energy per kilogram
Eincrease = 0.7 x 2.8x107
Eincrease = 19.6x106J
Ek(initial) = 0J
Ek(final) = Ek(initial) + Eincrease
Ek(final) = 19.6x106J
Ek(final) = mv2/2
v2 = 2Ek(vehicle)/m
v = [2Ek(vehicle)/m]1/2
v = [2x19.6x106/500]1/2
v = [78400]1/2
v = 280m/s
Note: It is not clear from the question whether the 500kg mass is that
of the vehicle and dummy after, or before, burning the fuel. To
get an answer exactly equal to 280m/s you seem to have to assume
that the 500kg is the mass after burning the fuel.
a.ii. u = 0m/s
v= 280m/s
t = 8s
a = ?
a = (v-u)/t
a = (280 -0)/8
a = 35m/s/s
s = ut +at2/2
s = 0 + 35x82/2
s = 1120m
b.i.
Fslope = component of gravitational force acting down the slope.
d. When moving up the slope: both Fslope and Ffriction are acting in
the same direction. This means that the unbalanced force causing
the acceleration between A and B is the sum of these two forces.
Funbalanced = Fslope + Ffriction
When moving down the slope: Ffriction acts up the slope, in the
opposite direction to Fslope. This means that the unbalanced force
causing the acceleration between B and C is the difference between
these two forces.
Funbalanced = Fslope - Ffriction
The acceleration is therefore greater when the trolley is moving up the slope.
2.a.i. Step 1 : Calculate the energy available from 0.7kg of fuel.
Eincrease = mass of fuel x energy per kilogram
Eincrease = 0.7 x 2.8x107
Eincrease = 19.6x106J
Ek(initial) = 0J
Ek(final) = Ek(initial) + Eincrease
Ek(final) = 19.6x106J
Ek(final) = mv2/2
v2 = 2Ek(vehicle)/m
v = [2Ek(vehicle)/m]1/2
v = [2x19.6x106/500]1/2
v = [78400]1/2
v = 280m/s
Note: It is not clear from the question whether the 500kg mass is that
of the vehicle and dummy after, or before, burning the fuel. To
get an answer exactly equal to 280m/s you seem to have to assume
that the 500kg is the mass after burning the fuel.
a.ii. u = 0m/s
v= 280m/s
t = 8s
a = ?
a = (v-u)/t
a = (280 -0)/8
a = 35m/s/s
s = ut +at2/2
s = 0 + 35x82/2
s = 1120m
b.i.
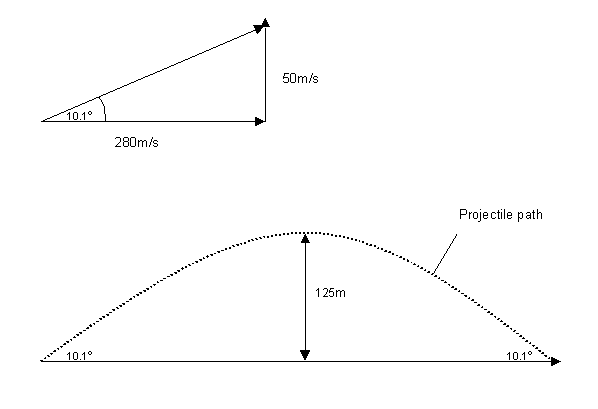 The horizontal velocity of the projectile is constant at 280m/s.
The vertical component of the motion will be up to a maximum
height and then fall back down to earth.
b.ii. The maximum height reached by the dummy will occur when the
vertical component(vver) of the velocity is zero.
vver2 = uver2 + 2asver
sver = (vver2 - uver2)/2a
sver = (02 - 502)/2x(-10)
sver = -2500/-20
sver = 125m
3.a. Step 1: calculate the time that the projectile takes to fall 0.8m.
sver = -0.8m
uver = 0m/s
aver = -10m/s/s
tver = ?
s = ut + at2/2
t2 = 2(s - ut)/a
t2 = 2(-0.8 - 0)/-10
t2 = 0.16s
t = 0.4s
vhor = shor/t
vhor = 0.2/0.4
vhor = 0.5m/s
3.b.i. Momentum before(Pbefore) = Momentum after(Pafter)
b.ii. mpelletupellet + mputtyuputty= (mpellet+mputty)v
5.0x10-4upellet+0.1x0 = (5.0x10-4+0.1)0.5
5.0x10-4upellet = 0.05025
upellet = 0.05025/5x10-4
upellet = 100.5m/s
c. Reducing the mass of the lump of putty will mean that after the collision
the pellet embedded in the putty will travel a greater horizontal displacement.
This will give a more accurate horizontal velocity, which in turn will give
a more accurate value of the pellets initial velocity.
The horizontal velocity of the projectile is constant at 280m/s.
The vertical component of the motion will be up to a maximum
height and then fall back down to earth.
b.ii. The maximum height reached by the dummy will occur when the
vertical component(vver) of the velocity is zero.
vver2 = uver2 + 2asver
sver = (vver2 - uver2)/2a
sver = (02 - 502)/2x(-10)
sver = -2500/-20
sver = 125m
3.a. Step 1: calculate the time that the projectile takes to fall 0.8m.
sver = -0.8m
uver = 0m/s
aver = -10m/s/s
tver = ?
s = ut + at2/2
t2 = 2(s - ut)/a
t2 = 2(-0.8 - 0)/-10
t2 = 0.16s
t = 0.4s
vhor = shor/t
vhor = 0.2/0.4
vhor = 0.5m/s
3.b.i. Momentum before(Pbefore) = Momentum after(Pafter)
b.ii. mpelletupellet + mputtyuputty= (mpellet+mputty)v
5.0x10-4upellet+0.1x0 = (5.0x10-4+0.1)0.5
5.0x10-4upellet = 0.05025
upellet = 0.05025/5x10-4
upellet = 100.5m/s
c. Reducing the mass of the lump of putty will mean that after the collision
the pellet embedded in the putty will travel a greater horizontal displacement.
This will give a more accurate horizontal velocity, which in turn will give
a more accurate value of the pellets initial velocity.
4.a.i.
| Pressure/kPa |
89 |
96 |
103 |
110 |
117 |
| Temperature/oC |
-20 |
0 |
20 |
40 |
60 |
| Temperature/K |
253 |
273 |
293 |
313 |
333 |
a.ii. Take each pair of pressure and temperature reading.
For each pair calculate P/T.
89x103/253 = 351.8 Pa/K
96x103/273 = 351.6 Pa/K
103x103/293 = 351.5 Pa/K
110x103/313 = 351.4 Pa/K
117x103/333 = 351.3 Pa/K
From these calculations it is clear that : P/T = Constant
a.iii.As the temperature increases the helium atoms have more kinetic energy.
With increased kinetic energy the atoms are moving faster and collide
with the container walls, and the pressure probe, more frequently
and forcefully. The pressure(force/area) therefore increases.
b.i. P/T = constant
T = P/constant
T = 24000Pa/(351.5Pa/K)
T = 68.3K
5.a.i.
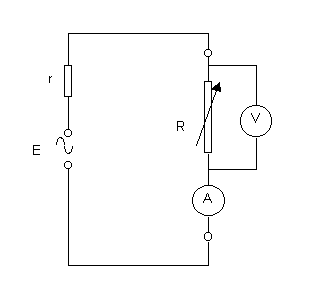 The variable resistor is connected across the audio output terminals.
The voltmeter is connected across this resistor and the ammeter measures
the current in the circuit.
a.ii. The internal resistance has a value equal to the negative gradient of
the graph.
r = -m
m = (y2- y1)/(x2- 1)
m = (2-1.2)/(0-0.5)
m = -1.6W
=>r=1.6W
a.iii.The emf of the supply is equal to the output voltage when there is no
current in the circuit.
E = 2.0V
I = E/(R+r)
I = 2.0/(4+1.6)
I = 0.357A
Vloudspeaker = IR
Vloudspeaker = 0.357x4
Vloudspeaker = 1.4V
b. When the voltage drop across the internal resistor and the calibrated
variable resistor is the same, as will be the case when the voltage
across the calibrated resistor is equal to half of the emf, the internal
resistor and the calibrated resistor must have the same value.
6.a.
The variable resistor is connected across the audio output terminals.
The voltmeter is connected across this resistor and the ammeter measures
the current in the circuit.
a.ii. The internal resistance has a value equal to the negative gradient of
the graph.
r = -m
m = (y2- y1)/(x2- 1)
m = (2-1.2)/(0-0.5)
m = -1.6W
=>r=1.6W
a.iii.The emf of the supply is equal to the output voltage when there is no
current in the circuit.
E = 2.0V
I = E/(R+r)
I = 2.0/(4+1.6)
I = 0.357A
Vloudspeaker = IR
Vloudspeaker = 0.357x4
Vloudspeaker = 1.4V
b. When the voltage drop across the internal resistor and the calibrated
variable resistor is the same, as will be the case when the voltage
across the calibrated resistor is equal to half of the emf, the internal
resistor and the calibrated resistor must have the same value.
6.a.
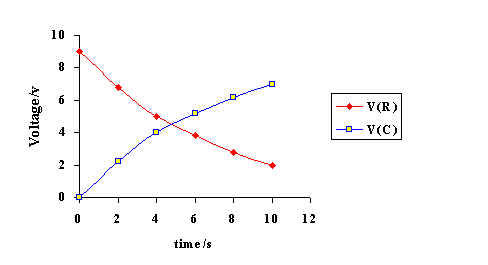 b. Vs = VR + Vc
VR = Vs - Vc
VR = 9-6
VR = 3V
I = VR/R
I = 3/6800
I = 441.2mA
c.i. When fully charged: Vc = 9V
Energy stored in capacitor = Energy dissipated in resistor
E = CV2/2
E = 1000x10-6x92/2
E = 40.5mJ
c.ii. The energy dissipated in the 20W resistor will be the
same as that dissipated in the 10W. This is because
the energy stored in the capacitor is still the same. The only difference
is that it will take longer for the capacitor to discharge when connected
across the 20W resistor.
7.a.i. Equate the energy gained from the electric field(Eelect) to the final kinetic
energy (Ek)of the electron.
Eelect = Ek
qV = mev2/2
v2 = 2qV/me
v2 = 2x1.6x10-19x5000/9.11x10-31
v2 = 1.75x1015
v = 41.9x106m/s
a.ii. v2 = (2qV/me)1/2
v2 = (2x1.6x10-19x2500/9.11x10-31)1/2
v2 = 29.6x106m/s
v1 = const x V11/2
v2 = const x (V1/2)1/2
v2/v1 = const x (V1/2)1/2/const x (V1)1/2
v2/v1 = 1/sqrt2
v2 = v1/sqrt2
b. Q = It (Q= total charge)
Nq = It (N = number of electrons & q = electronic charge)
N = It/q
N = 15x10-3x1/1.6x10-19
N = 9.375x1016
8.a.i. Vpk = 1.5x0.05
Vpk = 0.075V
a.ii. Rf/R1 = - Vout/Vin
Rf = -R1Vout/Vin
Rf = -10000x(0.9/-0.075)
Rf = 120000W
Rf = 120kW
b.i. Vout = (Rf/R1)(V2-V1)
Vout = (5x106/10x103)(0.4x10-3)
Vout = 500x0.40x10-3
Vout = 0.2V
b.ii. The differential amplifier amplifies the difference between the inverting
and non inverting input. The 50Hz mains signal will be input into both these
inputs and will therefore be filtered out. This will leave only the amplified
potential difference between the two pads.
9.a.i.
b. Vs = VR + Vc
VR = Vs - Vc
VR = 9-6
VR = 3V
I = VR/R
I = 3/6800
I = 441.2mA
c.i. When fully charged: Vc = 9V
Energy stored in capacitor = Energy dissipated in resistor
E = CV2/2
E = 1000x10-6x92/2
E = 40.5mJ
c.ii. The energy dissipated in the 20W resistor will be the
same as that dissipated in the 10W. This is because
the energy stored in the capacitor is still the same. The only difference
is that it will take longer for the capacitor to discharge when connected
across the 20W resistor.
7.a.i. Equate the energy gained from the electric field(Eelect) to the final kinetic
energy (Ek)of the electron.
Eelect = Ek
qV = mev2/2
v2 = 2qV/me
v2 = 2x1.6x10-19x5000/9.11x10-31
v2 = 1.75x1015
v = 41.9x106m/s
a.ii. v2 = (2qV/me)1/2
v2 = (2x1.6x10-19x2500/9.11x10-31)1/2
v2 = 29.6x106m/s
v1 = const x V11/2
v2 = const x (V1/2)1/2
v2/v1 = const x (V1/2)1/2/const x (V1)1/2
v2/v1 = 1/sqrt2
v2 = v1/sqrt2
b. Q = It (Q= total charge)
Nq = It (N = number of electrons & q = electronic charge)
N = It/q
N = 15x10-3x1/1.6x10-19
N = 9.375x1016
8.a.i. Vpk = 1.5x0.05
Vpk = 0.075V
a.ii. Rf/R1 = - Vout/Vin
Rf = -R1Vout/Vin
Rf = -10000x(0.9/-0.075)
Rf = 120000W
Rf = 120kW
b.i. Vout = (Rf/R1)(V2-V1)
Vout = (5x106/10x103)(0.4x10-3)
Vout = 500x0.40x10-3
Vout = 0.2V
b.ii. The differential amplifier amplifies the difference between the inverting
and non inverting input. The 50Hz mains signal will be input into both these
inputs and will therefore be filtered out. This will leave only the amplified
potential difference between the two pads.
9.a.i.
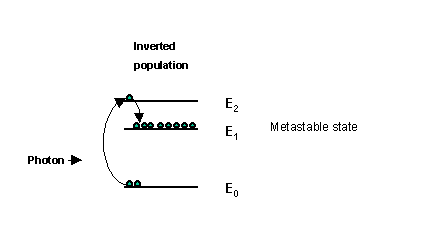 The high voltage pumps electrons up into energy state(E2) which then
fall into the metastable state E1 creating what is called an inverted
population. A passing photon, having an energy equal to the energy gap
E1 to E0 can encourage/stimulate an electron to drop from energy
state E1 to E2. This is the basis for stimulated emission.
Note: This energy level diagram is only an illustration to help with
the understanding of the concept of energy levels. Each different
laser will have a different energy level diagram.
a.ii. The fully reflecting mirror keeps all the photons in the laser cavity to
enable further stimulated emission. The partially reflecting mirror not
only ensures some reflection to sustain the stimulated emission but also
allows a narrow beam of laser light to leave the cavity.
b. Each bright spot occurs when the laser light interferes constructively.
This happens when the path difference, from each adjacent slit in
the diffraction grating to the screen, is a whole number of wavelengths.
In between the bright spots dark areas are produced when the laser light
interferes destructively. The laser light will completely cancel when the
path difference, from each adjacent slit in the diffraction grating to
the screen, is an odd number of wavelengths/2.
c. The energy from any laser light entering the eye is concentrated
into a very small area. This produces a very intense beam that will
produce significant damage to the retina.(I = P/A)
The energy emitted from a 100W lamp is spread over a much larger area.
This results in relatively low intensity light that will not result
in any damage to the eye.
d. I = P/A
P = E/t
=>I = E/At
I = 0.1/1.5x10-9x0.5x10-3
I = 133x109W/m2
10.a.i. qcritical = sin-1(1/n)
qcritical = sin-1(1/1.52)
qcritical = sin-1(0.658)
qcritical = 41.1o
a.ii.
The high voltage pumps electrons up into energy state(E2) which then
fall into the metastable state E1 creating what is called an inverted
population. A passing photon, having an energy equal to the energy gap
E1 to E0 can encourage/stimulate an electron to drop from energy
state E1 to E2. This is the basis for stimulated emission.
Note: This energy level diagram is only an illustration to help with
the understanding of the concept of energy levels. Each different
laser will have a different energy level diagram.
a.ii. The fully reflecting mirror keeps all the photons in the laser cavity to
enable further stimulated emission. The partially reflecting mirror not
only ensures some reflection to sustain the stimulated emission but also
allows a narrow beam of laser light to leave the cavity.
b. Each bright spot occurs when the laser light interferes constructively.
This happens when the path difference, from each adjacent slit in
the diffraction grating to the screen, is a whole number of wavelengths.
In between the bright spots dark areas are produced when the laser light
interferes destructively. The laser light will completely cancel when the
path difference, from each adjacent slit in the diffraction grating to
the screen, is an odd number of wavelengths/2.
c. The energy from any laser light entering the eye is concentrated
into a very small area. This produces a very intense beam that will
produce significant damage to the retina.(I = P/A)
The energy emitted from a 100W lamp is spread over a much larger area.
This results in relatively low intensity light that will not result
in any damage to the eye.
d. I = P/A
P = E/t
=>I = E/At
I = 0.1/1.5x10-9x0.5x10-3
I = 133x109W/m2
10.a.i. qcritical = sin-1(1/n)
qcritical = sin-1(1/1.52)
qcritical = sin-1(0.658)
qcritical = 41.1o
a.ii.
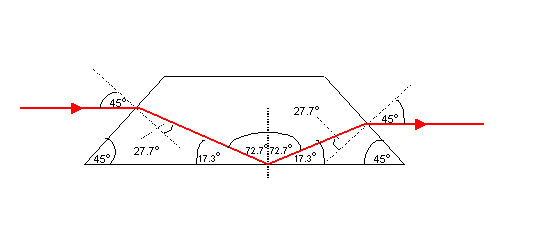 Note: This diagram has not been drawn to scale.
a.iii.
Note: This diagram has not been drawn to scale.
a.iii.
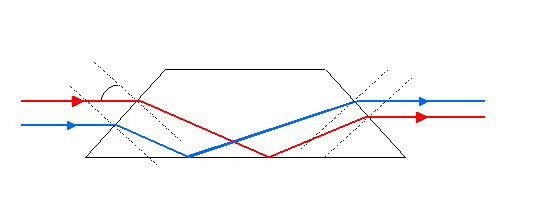 Angles have been omitted for clarity.
b. The image would be inverted.
11.a.i. Atomic number(Z) 95 = Number of protons in the nucleus.
Mass number(A) 241 = Number of protons + number of neutrons in the nucleus.
a.ii. 30kBq means that there are 30,000 nuclear disintegrations per second,
or equivalently, 30000 nuclei decay every second.
a.iii.Radiation can cause atoms or molecules to lose electrons and become
positive ions. These atoms, or molecules, have been ionised by the
ionising radiation.
a.iv. Use conservation of atomic and mass number to find the type of radiation.
Mass Number
241 = 237 + A
A = 4
Atomic number
95 = 93 + Z
z = 2
Radiation = 42He (alpha radiation)
a.v. Smoke detectors are usually located on the roof of rooms. This means that
any alpha radiation emitted will either be absorbed by the smoke detector
construction or the surrounding air, making it impossible for the radiation
to cause any biological damage.
b.i. Radioactive isotopes contained in natural rocks or soil contribute to
background radiation.
b.ii. Total absorbed dose = dose per detector x number of detectors
Total absorbed dose = 1.2x10-8x15000
Total absorbed dose = 180mGy
Dose equivalent = Absorbed dose x Quality factor
H = DQ
H = 180x10-6x20
H = 3.6mSv
The permissible level of 5mSv per year is NOT exceeded.
Angles have been omitted for clarity.
b. The image would be inverted.
11.a.i. Atomic number(Z) 95 = Number of protons in the nucleus.
Mass number(A) 241 = Number of protons + number of neutrons in the nucleus.
a.ii. 30kBq means that there are 30,000 nuclear disintegrations per second,
or equivalently, 30000 nuclei decay every second.
a.iii.Radiation can cause atoms or molecules to lose electrons and become
positive ions. These atoms, or molecules, have been ionised by the
ionising radiation.
a.iv. Use conservation of atomic and mass number to find the type of radiation.
Mass Number
241 = 237 + A
A = 4
Atomic number
95 = 93 + Z
z = 2
Radiation = 42He (alpha radiation)
a.v. Smoke detectors are usually located on the roof of rooms. This means that
any alpha radiation emitted will either be absorbed by the smoke detector
construction or the surrounding air, making it impossible for the radiation
to cause any biological damage.
b.i. Radioactive isotopes contained in natural rocks or soil contribute to
background radiation.
b.ii. Total absorbed dose = dose per detector x number of detectors
Total absorbed dose = 1.2x10-8x15000
Total absorbed dose = 180mGy
Dose equivalent = Absorbed dose x Quality factor
H = DQ
H = 180x10-6x20
H = 3.6mSv
The permissible level of 5mSv per year is NOT exceeded.
END OF QUESTION PAPER
Return to past paper index page.


c.
Fslope = component of gravitational force acting down the slope. d. When moving up the slope: both Fslope and Ffriction are acting in the same direction. This means that the unbalanced force causing the acceleration between A and B is the sum of these two forces. Funbalanced = Fslope + Ffriction When moving down the slope: Ffriction acts up the slope, in the opposite direction to Fslope. This means that the unbalanced force causing the acceleration between B and C is the difference between these two forces. Funbalanced = Fslope - Ffriction The acceleration is therefore greater when the trolley is moving up the slope. 2.a.i. Step 1 : Calculate the energy available from 0.7kg of fuel. Eincrease = mass of fuel x energy per kilogram Eincrease = 0.7 x 2.8x107 Eincrease = 19.6x106J Ek(initial) = 0J Ek(final) = Ek(initial) + Eincrease Ek(final) = 19.6x106J Ek(final) = mv2/2 v2 = 2Ek(vehicle)/m v = [2Ek(vehicle)/m]1/2 v = [2x19.6x106/500]1/2 v = [78400]1/2 v = 280m/s Note: It is not clear from the question whether the 500kg mass is that of the vehicle and dummy after, or before, burning the fuel. To get an answer exactly equal to 280m/s you seem to have to assume that the 500kg is the mass after burning the fuel. a.ii. u = 0m/s v= 280m/s t = 8s a = ? a = (v-u)/t a = (280 -0)/8 a = 35m/s/s s = ut +at2/2 s = 0 + 35x82/2 s = 1120m b.i.
The horizontal velocity of the projectile is constant at 280m/s. The vertical component of the motion will be up to a maximum height and then fall back down to earth. b.ii. The maximum height reached by the dummy will occur when the vertical component(vver) of the velocity is zero. vver2 = uver2 + 2asver sver = (vver2 - uver2)/2a sver = (02 - 502)/2x(-10) sver = -2500/-20 sver = 125m 3.a. Step 1: calculate the time that the projectile takes to fall 0.8m. sver = -0.8m uver = 0m/s aver = -10m/s/s tver = ? s = ut + at2/2 t2 = 2(s - ut)/a t2 = 2(-0.8 - 0)/-10 t2 = 0.16s t = 0.4s vhor = shor/t vhor = 0.2/0.4 vhor = 0.5m/s 3.b.i. Momentum before(Pbefore) = Momentum after(Pafter) b.ii. mpelletupellet + mputtyuputty= (mpellet+mputty)v 5.0x10-4upellet+0.1x0 = (5.0x10-4+0.1)0.5 5.0x10-4upellet = 0.05025 upellet = 0.05025/5x10-4 upellet = 100.5m/s c. Reducing the mass of the lump of putty will mean that after the collision the pellet embedded in the putty will travel a greater horizontal displacement. This will give a more accurate horizontal velocity, which in turn will give a more accurate value of the pellets initial velocity.
The variable resistor is connected across the audio output terminals. The voltmeter is connected across this resistor and the ammeter measures the current in the circuit. a.ii. The internal resistance has a value equal to the negative gradient of the graph. r = -m m = (y2- y1)/(x2- 1) m = (2-1.2)/(0-0.5) m = -1.6W =>r=1.6W a.iii.The emf of the supply is equal to the output voltage when there is no current in the circuit. E = 2.0V I = E/(R+r) I = 2.0/(4+1.6) I = 0.357A Vloudspeaker = IR Vloudspeaker = 0.357x4 Vloudspeaker = 1.4V b. When the voltage drop across the internal resistor and the calibrated variable resistor is the same, as will be the case when the voltage across the calibrated resistor is equal to half of the emf, the internal resistor and the calibrated resistor must have the same value. 6.a.
b. Vs = VR + Vc VR = Vs - Vc VR = 9-6 VR = 3V I = VR/R I = 3/6800 I = 441.2mA c.i. When fully charged: Vc = 9V Energy stored in capacitor = Energy dissipated in resistor E = CV2/2 E = 1000x10-6x92/2 E = 40.5mJ c.ii. The energy dissipated in the 20W resistor will be the same as that dissipated in the 10W. This is because the energy stored in the capacitor is still the same. The only difference is that it will take longer for the capacitor to discharge when connected across the 20W resistor. 7.a.i. Equate the energy gained from the electric field(Eelect) to the final kinetic energy (Ek)of the electron. Eelect = Ek qV = mev2/2 v2 = 2qV/me v2 = 2x1.6x10-19x5000/9.11x10-31 v2 = 1.75x1015 v = 41.9x106m/s a.ii. v2 = (2qV/me)1/2 v2 = (2x1.6x10-19x2500/9.11x10-31)1/2 v2 = 29.6x106m/s v1 = const x V11/2 v2 = const x (V1/2)1/2 v2/v1 = const x (V1/2)1/2/const x (V1)1/2 v2/v1 = 1/sqrt2 v2 = v1/sqrt2 b. Q = It (Q= total charge) Nq = It (N = number of electrons & q = electronic charge) N = It/q N = 15x10-3x1/1.6x10-19 N = 9.375x1016 8.a.i. Vpk = 1.5x0.05 Vpk = 0.075V a.ii. Rf/R1 = - Vout/Vin Rf = -R1Vout/Vin Rf = -10000x(0.9/-0.075) Rf = 120000W Rf = 120kW b.i. Vout = (Rf/R1)(V2-V1) Vout = (5x106/10x103)(0.4x10-3) Vout = 500x0.40x10-3 Vout = 0.2V b.ii. The differential amplifier amplifies the difference between the inverting and non inverting input. The 50Hz mains signal will be input into both these inputs and will therefore be filtered out. This will leave only the amplified potential difference between the two pads. 9.a.i.
The high voltage pumps electrons up into energy state(E2) which then fall into the metastable state E1 creating what is called an inverted population. A passing photon, having an energy equal to the energy gap E1 to E0 can encourage/stimulate an electron to drop from energy state E1 to E2. This is the basis for stimulated emission. Note: This energy level diagram is only an illustration to help with the understanding of the concept of energy levels. Each different laser will have a different energy level diagram. a.ii. The fully reflecting mirror keeps all the photons in the laser cavity to enable further stimulated emission. The partially reflecting mirror not only ensures some reflection to sustain the stimulated emission but also allows a narrow beam of laser light to leave the cavity. b. Each bright spot occurs when the laser light interferes constructively. This happens when the path difference, from each adjacent slit in the diffraction grating to the screen, is a whole number of wavelengths. In between the bright spots dark areas are produced when the laser light interferes destructively. The laser light will completely cancel when the path difference, from each adjacent slit in the diffraction grating to the screen, is an odd number of wavelengths/2. c. The energy from any laser light entering the eye is concentrated into a very small area. This produces a very intense beam that will produce significant damage to the retina.(I = P/A) The energy emitted from a 100W lamp is spread over a much larger area. This results in relatively low intensity light that will not result in any damage to the eye. d. I = P/A P = E/t =>I = E/At I = 0.1/1.5x10-9x0.5x10-3 I = 133x109W/m2 10.a.i. qcritical = sin-1(1/n) qcritical = sin-1(1/1.52) qcritical = sin-1(0.658) qcritical = 41.1o a.ii.
Note: This diagram has not been drawn to scale. a.iii.
Angles have been omitted for clarity. b. The image would be inverted. 11.a.i. Atomic number(Z) 95 = Number of protons in the nucleus. Mass number(A) 241 = Number of protons + number of neutrons in the nucleus. a.ii. 30kBq means that there are 30,000 nuclear disintegrations per second, or equivalently, 30000 nuclei decay every second. a.iii.Radiation can cause atoms or molecules to lose electrons and become positive ions. These atoms, or molecules, have been ionised by the ionising radiation. a.iv. Use conservation of atomic and mass number to find the type of radiation. Mass Number 241 = 237 + A A = 4 Atomic number 95 = 93 + Z z = 2 Radiation = 42He (alpha radiation) a.v. Smoke detectors are usually located on the roof of rooms. This means that any alpha radiation emitted will either be absorbed by the smoke detector construction or the surrounding air, making it impossible for the radiation to cause any biological damage. b.i. Radioactive isotopes contained in natural rocks or soil contribute to background radiation. b.ii. Total absorbed dose = dose per detector x number of detectors Total absorbed dose = 1.2x10-8x15000 Total absorbed dose = 180mGy Dose equivalent = Absorbed dose x Quality factor H = DQ H = 180x10-6x20 H = 3.6mSv The permissible level of 5mSv per year is NOT exceeded.