
1992 Higher Physics Paper I Solutions
Return to Higher Physics past paper index page.
1. E 11. E 21. B
2. A 12. B 22. C
3. C 13. D 23. C
4. C 14. D 24. B
5. E 15. A 25. A
6. E 16. B 26. B
7. B 17. B 27. D
8. C 18. A 28. C
9. E 19. B 29. C
10.E 20. E 30. C
31. Draw a scaled diagram or use trigonometry/Pythagoras' theorem to solve.
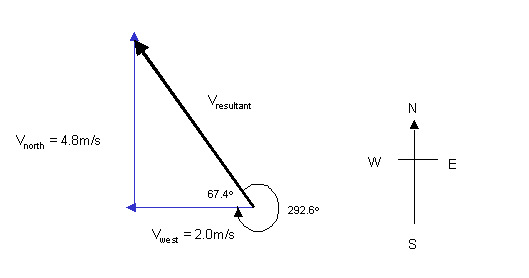 Vresultant2 = Vnorth2+Vwest2
Vresultant2 = 4.82+2.02
Vresultant2 = 23.04+4.0
Vresultant2 = 27.04
Vresultant = 5.2m/s
tanq = Vnorth/Vwest
tanq = 4.8/2
tanq = 2.4
q = tan-12.4
q = 67.4o
Vresultant = 5.2m/s at a bearing of 292.6o
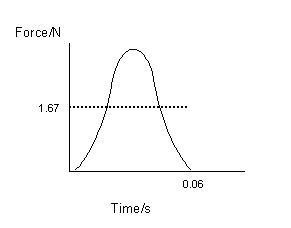
32.a. Favg = DP/t
Favg = m(v-u)/t
m = 0.05kg
u = 0m/s
v = 2.0m/s
t = 0.060s
Favg = 0.05(2.0-0)/0.06
Favg = 1.67N
b.
Vresultant2 = Vnorth2+Vwest2
Vresultant2 = 4.82+2.02
Vresultant2 = 23.04+4.0
Vresultant2 = 27.04
Vresultant = 5.2m/s
tanq = Vnorth/Vwest
tanq = 4.8/2
tanq = 2.4
q = tan-12.4
q = 67.4o
Vresultant = 5.2m/s at a bearing of 292.6o
32.a. Favg = DP/t
Favg = m(v-u)/t
m = 0.05kg
u = 0m/s
v = 2.0m/s
t = 0.060s
Favg = 0.05(2.0-0)/0.06
Favg = 1.67N
b.
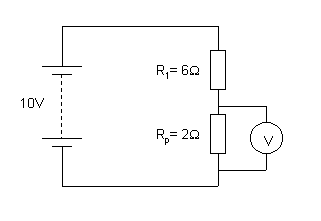
 33.a. Vmeter = [R1/(R1+R2)]xVsupply
Vmeter = [6/(6+6)]x10
Vmeter = 5V
This answer is obvious because the voltage splits up evenly
across the 6W resistors.
b. Calculate the resistance of the 3W and 6W parallel network.
1/Rp = 1/R1 + 1/R2
1/Rp = 1/6 +1/3
1/Rp = 3/6
Rp = 6/3 = 2W
The circuit can therefore be reduced to that below.
33.a. Vmeter = [R1/(R1+R2)]xVsupply
Vmeter = [6/(6+6)]x10
Vmeter = 5V
This answer is obvious because the voltage splits up evenly
across the 6W resistors.
b. Calculate the resistance of the 3W and 6W parallel network.
1/Rp = 1/R1 + 1/R2
1/Rp = 1/6 +1/3
1/Rp = 3/6
Rp = 6/3 = 2W
The circuit can therefore be reduced to that below.
 Where the 2W resistor represents the parallel network.
The voltmeter reading can now be calculated.
Vmeter = [Rp/(R1+Rp)]xVsupply
Vmeter = [2/(6+2)]x10
Vmeter = 2.5V
This problem can also be solved using ohm's law.
34. Each half of the loop has a resistance of 15W. These half loops
are like two resistors of equal value in parallel. Using this
analysis allows Rp to be calculated.
Rp = R/N
Rp = 15/2
Rp = 7.5W
35.a. This is an example of a nuclear fission reaction.
b. The total mass of the reactants is greater than the mass of
the products. This "missing mass" also called the mass defect
is converted into energy.
The energy released can be calculated using E = mc2, where m
is the missing mass value in kilograms.
36.
Where the 2W resistor represents the parallel network.
The voltmeter reading can now be calculated.
Vmeter = [Rp/(R1+Rp)]xVsupply
Vmeter = [2/(6+2)]x10
Vmeter = 2.5V
This problem can also be solved using ohm's law.
34. Each half of the loop has a resistance of 15W. These half loops
are like two resistors of equal value in parallel. Using this
analysis allows Rp to be calculated.
Rp = R/N
Rp = 15/2
Rp = 7.5W
35.a. This is an example of a nuclear fission reaction.
b. The total mass of the reactants is greater than the mass of
the products. This "missing mass" also called the mass defect
is converted into energy.
The energy released can be calculated using E = mc2, where m
is the missing mass value in kilograms.
36.
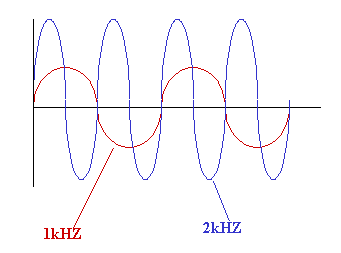 To increase the current in the circuit, as the supply frequency is
increased, the voltage across the resistor must increase.
37.a. E4 to E0 will produce the highest energy/frequency radiation.
b. DE = E4 - E0
DE = hf
f = DE/h
f = (E4 - E0)/h
f = [-0.864x10-19-(-21.76x10-19)]/6.63x10-34
f = 20.896x10-19/6.63x10-34
f = 3.15x1015Hz
To increase the current in the circuit, as the supply frequency is
increased, the voltage across the resistor must increase.
37.a. E4 to E0 will produce the highest energy/frequency radiation.
b. DE = E4 - E0
DE = hf
f = DE/h
f = (E4 - E0)/h
f = [-0.864x10-19-(-21.76x10-19)]/6.63x10-34
f = 20.896x10-19/6.63x10-34
f = 3.15x1015Hz
END OF QUESTION PAPER
Return to Higher Physics past paper index page.


Vresultant2 = Vnorth2+Vwest2 Vresultant2 = 4.82+2.02 Vresultant2 = 23.04+4.0 Vresultant2 = 27.04 Vresultant = 5.2m/s tanq = Vnorth/Vwest tanq = 4.8/2 tanq = 2.4 q = tan-12.4 q = 67.4o Vresultant = 5.2m/s at a bearing of 292.6o 32.a. Favg = DP/t Favg = m(v-u)/t m = 0.05kg u = 0m/s v = 2.0m/s t = 0.060s Favg = 0.05(2.0-0)/0.06 Favg = 1.67N b.
33.a. Vmeter = [R1/(R1+R2)]xVsupply Vmeter = [6/(6+6)]x10 Vmeter = 5V This answer is obvious because the voltage splits up evenly across the 6W resistors. b. Calculate the resistance of the 3W and 6W parallel network. 1/Rp = 1/R1 + 1/R2 1/Rp = 1/6 +1/3 1/Rp = 3/6 Rp = 6/3 = 2W The circuit can therefore be reduced to that below.
Where the 2W resistor represents the parallel network. The voltmeter reading can now be calculated. Vmeter = [Rp/(R1+Rp)]xVsupply Vmeter = [2/(6+2)]x10 Vmeter = 2.5V This problem can also be solved using ohm's law. 34. Each half of the loop has a resistance of 15W. These half loops are like two resistors of equal value in parallel. Using this analysis allows Rp to be calculated. Rp = R/N Rp = 15/2 Rp = 7.5W 35.a. This is an example of a nuclear fission reaction. b. The total mass of the reactants is greater than the mass of the products. This "missing mass" also called the mass defect is converted into energy. The energy released can be calculated using E = mc2, where m is the missing mass value in kilograms. 36.
To increase the current in the circuit, as the supply frequency is increased, the voltage across the resistor must increase. 37.a. E4 to E0 will produce the highest energy/frequency radiation. b. DE = E4 - E0 DE = hf f = DE/h f = (E4 - E0)/h f = [-0.864x10-19-(-21.76x10-19)]/6.63x10-34 f = 20.896x10-19/6.63x10-34 f = 3.15x1015Hz