In the 1920s, Edwin Hubble had access to the Hooker telescope on Mount Wilson, Los Angeles. This was the largest telescope in the world at that time. His first breakthrough was the discovery of a cepheid variable star in the Andromeda nebula. This enabled him to calculate the distance to Andromeda and he quickly realised this was not a nebula but a galaxy outside the Milky Way.
This video follows his work.
Hubble – nebulae or galaxies? from mr mackenzie on Vimeo.
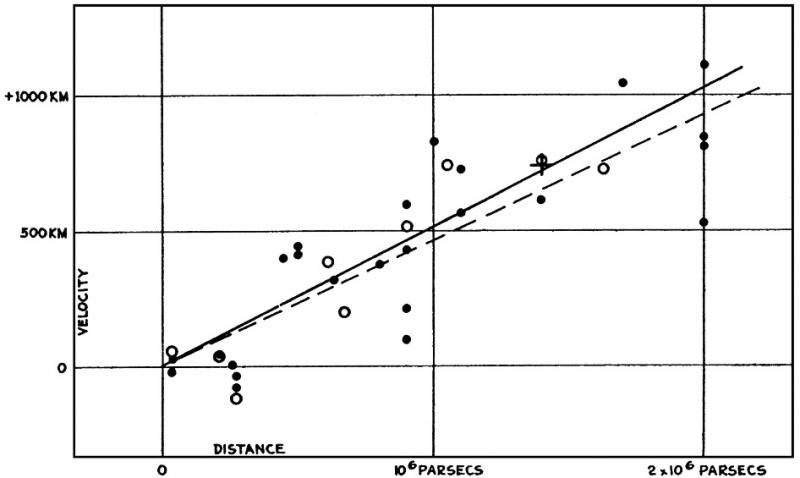
Hubble then turned his attention to other galaxies, looking for cepheid variable stars that would allow him to determine their distances from the Milky Way. He used redshift to calculate their recession velocity and plotted a graph against their distance from us.
He found that the recession velocity (v) was directly proportional to distance (d). We can express this relationship as
which is known as Hubble’s law, where is the Hubble constant. Astronomers agree that the current value of the Hubble constant is
.
Since this is a SQA course, we need to convert the constant into SI units – giving
In this second video, Professor Jim Al-Khalili looks at Hubble’s work on measuring redshift for different galaxies and his discovery of an expanding universe.
Hubble’s discovery of the expanding universe from mr mackenzie on Vimeo.
Although he was American, Edwin Hubble transformed himself into a tea drinking, pipe smoking, tweed wearing Englishman during his time as a Rhodes Scholar at Oxford. He probably wouldn’t approve of this last video.
It is said that when Hubble died, he left his collection of tweed jackets to Mr Jamieson-Caley.
Unfortunately, astronomers were not eligible for the Nobel Prize for Physics while Hubble was alive. The rules have now been changed.