
Solutions to SQA examination
1995 Higher Grade Physics
Paper II Solutions
Return to past paper index page.
1.a. Vectors have magnitude and direction, whereas, scalars have magnitude only.
b.i.
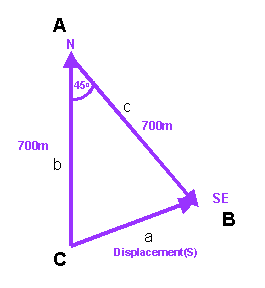 Use the cosine rule to calculate the magnitude of the displacement.
a2 = b2 + c2 -2bcCosA
a2 = 7002 + 7002 -2x700x700Cos45o
a2 = 980000 - 692964.65
a2 = 287035.35
a = 535.7m
As the triangle is isosceles angles B and C are equal in size.
Angle C = (180 - 45)/2 = 67.5o
Displacement (s) = 535.7m at a bearing of 067.5o
b.ii. Velocity(v) = Displacement(s)/Time(t)
vandy =535.7/t
t1 = Total distance(d)/Speed
t1 = 1400/3
t1 = 466.67s
=>vAndy = 535.7/466.67
vAndy = 1.15m/s
The velocity bearing is also 067.5o
v = 1.15m/s (067.5o)
b.iii.vPaul = 2.5s (067.5o)
b.iv. t2 = Total distance(d)/Speed
t2 = 535.7/2.5
t2 = 215.1s
Including Paul's five minutes waiting time the total time(ttotal))
for Pauls journey, in seconds, is can be calculated.
ttotal) = t2 + 215.1
ttotal) = 5x60 + 215.1
ttotal) = 515.1s
Pauls total time = 515.1s
Andy's journey time(t1) = 466.67s
Andy reaches the checkpoint ahead of Paul by 48.4s
2.a. Sprinters P and Q have the same journey time.
For sprinter P:
s = 20m
a = 1.6m/s/s
u = 0m/s
t = ?
Use: s = ut + 1/2(at2)
20 = 0xt + 1/2(1.6xt2)
t2 = 20/0.8
t2 = 25
t = 5s
The time for both sprinters is 5s
b. vP = u + at
vP = 0 + 1.6x5
vP = 8m/s
vQ = u + at
vQ = 0 + 1.2x5
vQ = 6m/s
c. To calculate the displacement of Q from their starting point
to the finishing line use: s = ut + 1/2(at2).
s = 0xt + 1/2(1.2x52)
s = 15m
The distance between starting points is therefore 5m
3.a.i. Initially the sand filled box is at rest and has no kinetic energy.
The bullet embeds itself in the sand filled box and its kinetic
energy is shared with the box. This constitutes an inelastic collision
and kinetic energy is not conserved. However, after this event the kinetic
energy of the bullet and box system can be calculated using the
principle of conservation of energy.
This means that the potential energy gain of the bullet and box, at their
maximum height, is equal to the initial kinetic energy of the bullet
and box.
Note: the bullet and box have no kinetic energy at the maximum height.
Epgain = Ekinitial
mgh = 1/2(mv2)
v2 = 2gh
v2 = 2x9.8x0.1
v2 = 1.96
v = 1.4m/s
a.ii. To solve this problem apply the law of conservation of linear momentum.
Momentum before(Pbefore) = Momentum after(Pafter)
mbulletubullet + mboxubox= (mbullet+mbox)v
The initial velocity of the box is zero therefore the term with this value
can be ignored.
ubullet = (mbullet+mbox)v/mbullet
ubullet = (10x1.4)/0.025
ubullet = 560m/s
b. The change in momentum of the bullet in this collision will be greater
than in the first experiment. To conserve momentum this means that the
change in momentum of the box of sand will also be greater. The only way
that this change in momentum can be increased is if the box moves off with
a greater velocity. The box thus has a greater initial kinetic energy
that will be transferred into potential energy resulting in the box reaching
a greater height.
4.a. The tension force provided by the cable will be equal in size to the weight
of the block, but act in the opposite direction.
Use the cosine rule to calculate the magnitude of the displacement.
a2 = b2 + c2 -2bcCosA
a2 = 7002 + 7002 -2x700x700Cos45o
a2 = 980000 - 692964.65
a2 = 287035.35
a = 535.7m
As the triangle is isosceles angles B and C are equal in size.
Angle C = (180 - 45)/2 = 67.5o
Displacement (s) = 535.7m at a bearing of 067.5o
b.ii. Velocity(v) = Displacement(s)/Time(t)
vandy =535.7/t
t1 = Total distance(d)/Speed
t1 = 1400/3
t1 = 466.67s
=>vAndy = 535.7/466.67
vAndy = 1.15m/s
The velocity bearing is also 067.5o
v = 1.15m/s (067.5o)
b.iii.vPaul = 2.5s (067.5o)
b.iv. t2 = Total distance(d)/Speed
t2 = 535.7/2.5
t2 = 215.1s
Including Paul's five minutes waiting time the total time(ttotal))
for Pauls journey, in seconds, is can be calculated.
ttotal) = t2 + 215.1
ttotal) = 5x60 + 215.1
ttotal) = 515.1s
Pauls total time = 515.1s
Andy's journey time(t1) = 466.67s
Andy reaches the checkpoint ahead of Paul by 48.4s
2.a. Sprinters P and Q have the same journey time.
For sprinter P:
s = 20m
a = 1.6m/s/s
u = 0m/s
t = ?
Use: s = ut + 1/2(at2)
20 = 0xt + 1/2(1.6xt2)
t2 = 20/0.8
t2 = 25
t = 5s
The time for both sprinters is 5s
b. vP = u + at
vP = 0 + 1.6x5
vP = 8m/s
vQ = u + at
vQ = 0 + 1.2x5
vQ = 6m/s
c. To calculate the displacement of Q from their starting point
to the finishing line use: s = ut + 1/2(at2).
s = 0xt + 1/2(1.2x52)
s = 15m
The distance between starting points is therefore 5m
3.a.i. Initially the sand filled box is at rest and has no kinetic energy.
The bullet embeds itself in the sand filled box and its kinetic
energy is shared with the box. This constitutes an inelastic collision
and kinetic energy is not conserved. However, after this event the kinetic
energy of the bullet and box system can be calculated using the
principle of conservation of energy.
This means that the potential energy gain of the bullet and box, at their
maximum height, is equal to the initial kinetic energy of the bullet
and box.
Note: the bullet and box have no kinetic energy at the maximum height.
Epgain = Ekinitial
mgh = 1/2(mv2)
v2 = 2gh
v2 = 2x9.8x0.1
v2 = 1.96
v = 1.4m/s
a.ii. To solve this problem apply the law of conservation of linear momentum.
Momentum before(Pbefore) = Momentum after(Pafter)
mbulletubullet + mboxubox= (mbullet+mbox)v
The initial velocity of the box is zero therefore the term with this value
can be ignored.
ubullet = (mbullet+mbox)v/mbullet
ubullet = (10x1.4)/0.025
ubullet = 560m/s
b. The change in momentum of the bullet in this collision will be greater
than in the first experiment. To conserve momentum this means that the
change in momentum of the box of sand will also be greater. The only way
that this change in momentum can be increased is if the box moves off with
a greater velocity. The box thus has a greater initial kinetic energy
that will be transferred into potential energy resulting in the box reaching
a greater height.
4.a. The tension force provided by the cable will be equal in size to the weight
of the block, but act in the opposite direction.
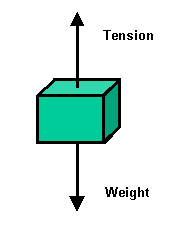 W = ? w = mg
m =5.0x103kg w = 5.0x103x9.8
g = 9.8N/kg w = 49000N
b.i.
W = ? w = mg
m =5.0x103kg w = 5.0x103x9.8
g = 9.8N/kg w = 49000N
b.i.
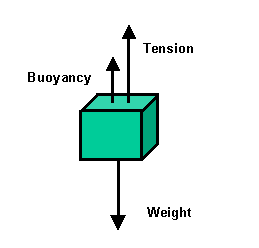 Weight(W) = Tension(T) + Buoyancy(B)
T = W - B
B = W - T
B = 49000 - 29000
B = 20000N
b.ii. The pressure acting on the lower surface of the block is greater than
the pressure acting on the upper surface, because the lower surface is
at a greater depth.
Weight(W) = Tension(T) + Buoyancy(B)
T = W - B
B = W - T
B = 49000 - 29000
B = 20000N
b.ii. The pressure acting on the lower surface of the block is greater than
the pressure acting on the upper surface, because the lower surface is
at a greater depth.
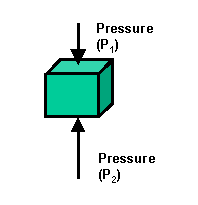 As the force on each surface is given by the equation F = PA, the
upward force is greater than the downward force. This net upward
force is called buoyancy or upthrust.
c. The pressure difference will be the same at all depths. This will result
in the upthrust being the same at any depth.
5.a. The circuit in the problem can be drawn in the more familiar form as
shown in the diagram below.
As the force on each surface is given by the equation F = PA, the
upward force is greater than the downward force. This net upward
force is called buoyancy or upthrust.
c. The pressure difference will be the same at all depths. This will result
in the upthrust being the same at any depth.
5.a. The circuit in the problem can be drawn in the more familiar form as
shown in the diagram below.
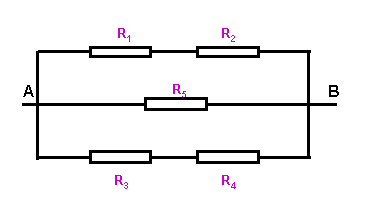 R1 is in series with R2
R1+2 = 20W
R3 is in series with R4
R3+4 = 20W
R1+2, R3+4 and R5 are in parallel.
1/Rtotal = 1/R1+2 + 1/R1+2 + 1/R5
1/Rtotal = 1/20 +1/20 +1/10
1/Rtotal = 4/20
Rtotal = 20/4 = 5W
b.i. The greatest current will flow through R5 thus this is
where the greatest power will develop.
b.ii. IR5 = V/R5
IR5 = 12/10
IR5 = 1.2A
P = IR52R5
P = 1.22x10
P = 14.4W
c.i. The electric potential is the same at points A and C. With no
no potential difference across R5 no current will be
flowing through it.
c.ii. Resistors R1 and R2 are in series. The current
flowing through branch BCD can be calculated using ohms law.
IBCD = VBD/R2+3
IBCD = 12/20
IBCD = 0.6A
Similarly the current flowing through branch BAD can be calculated.
IBAD = VBD/R2+3
IBAD = 12/20
IBAD = 0.6A
Ibattery = IBCD + IBAD
Ibattery = 0.6 + 0.6
Ibattery = 1.2A
6.a. "Lost volts" = Ir
"Lost volts" = 0.5x.2
"Lost volts" = 0.1V
emf(E) = Terminal Potential Difference(Vtpd) + "Lost volts"
Vtpd = V1
V1 = E - "Lost volts"
V1 = 12.0 - 0.1
V1 = 11.9V
7.a. E = I(R+r)
E/I = R+r
R = E/I-r As required
b.i. The above equation can be written as: R = E(1/I) - r
Compare this to: y = mx + c
The y-intercept(c) is equal to -r.
The gradient(m) is equal to E.
c = -2.5
=>r = 2.5W
b.ii. m = (y2-y1)/(x2-x1)
m = (6-0)/(0.5-0.15)
m = 6/0.35
m = 17.1
=>E = 17.1V
c. I = E/r
I = 17.1/2.5
I = 6.8A
8.a. The minimum energy an electron needs to absorb to escape from an atom
is called the work function.
b.i. Ephoton = hf
Ephoton = 6.63x10-34x6.1x1014
Ephoton = 4.04x10-19J
Emax. kinetic = Ephoton - Ework
Emax. kinetic = 4.04x10-19 - 3.04x10-19
Emax. kinetic = 1.00x10-19J
b.ii. Ektotal = Emax. kinetic + Efield
Note: Efield is the energy gained by the electron in the
electric field.
Efield = qV
Efield = 1.6x10-19x0.8
Efield = 1.28x10-19
Ektotal = 1.00x10-19 + 1.28x10-19
Ektotal = 2.28x10-19J
c. To stop the photoelectrons the wok done by the electric field
must equal the maximum kinetic energy of the photoelectrons.
Efield = Emax. kinetic
qV = Emax. kinetic
V = Emax. kinetic/q
V = 1.00x10-19/1.6x10-19
V = 0.625V
9.a. qcrit = sin-1(1/n)
qcrit = sin-1(1/1.33)
qcrit = sin-1(0.752)
qcrit = 48.7o
R1 is in series with R2
R1+2 = 20W
R3 is in series with R4
R3+4 = 20W
R1+2, R3+4 and R5 are in parallel.
1/Rtotal = 1/R1+2 + 1/R1+2 + 1/R5
1/Rtotal = 1/20 +1/20 +1/10
1/Rtotal = 4/20
Rtotal = 20/4 = 5W
b.i. The greatest current will flow through R5 thus this is
where the greatest power will develop.
b.ii. IR5 = V/R5
IR5 = 12/10
IR5 = 1.2A
P = IR52R5
P = 1.22x10
P = 14.4W
c.i. The electric potential is the same at points A and C. With no
no potential difference across R5 no current will be
flowing through it.
c.ii. Resistors R1 and R2 are in series. The current
flowing through branch BCD can be calculated using ohms law.
IBCD = VBD/R2+3
IBCD = 12/20
IBCD = 0.6A
Similarly the current flowing through branch BAD can be calculated.
IBAD = VBD/R2+3
IBAD = 12/20
IBAD = 0.6A
Ibattery = IBCD + IBAD
Ibattery = 0.6 + 0.6
Ibattery = 1.2A
6.a. "Lost volts" = Ir
"Lost volts" = 0.5x.2
"Lost volts" = 0.1V
emf(E) = Terminal Potential Difference(Vtpd) + "Lost volts"
Vtpd = V1
V1 = E - "Lost volts"
V1 = 12.0 - 0.1
V1 = 11.9V
7.a. E = I(R+r)
E/I = R+r
R = E/I-r As required
b.i. The above equation can be written as: R = E(1/I) - r
Compare this to: y = mx + c
The y-intercept(c) is equal to -r.
The gradient(m) is equal to E.
c = -2.5
=>r = 2.5W
b.ii. m = (y2-y1)/(x2-x1)
m = (6-0)/(0.5-0.15)
m = 6/0.35
m = 17.1
=>E = 17.1V
c. I = E/r
I = 17.1/2.5
I = 6.8A
8.a. The minimum energy an electron needs to absorb to escape from an atom
is called the work function.
b.i. Ephoton = hf
Ephoton = 6.63x10-34x6.1x1014
Ephoton = 4.04x10-19J
Emax. kinetic = Ephoton - Ework
Emax. kinetic = 4.04x10-19 - 3.04x10-19
Emax. kinetic = 1.00x10-19J
b.ii. Ektotal = Emax. kinetic + Efield
Note: Efield is the energy gained by the electron in the
electric field.
Efield = qV
Efield = 1.6x10-19x0.8
Efield = 1.28x10-19
Ektotal = 1.00x10-19 + 1.28x10-19
Ektotal = 2.28x10-19J
c. To stop the photoelectrons the wok done by the electric field
must equal the maximum kinetic energy of the photoelectrons.
Efield = Emax. kinetic
qV = Emax. kinetic
V = Emax. kinetic/q
V = 1.00x10-19/1.6x10-19
V = 0.625V
9.a. qcrit = sin-1(1/n)
qcrit = sin-1(1/1.33)
qcrit = sin-1(0.752)
qcrit = 48.7o
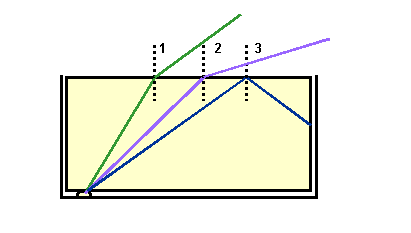 Note: Some internal reflection occurs for the light incident at
the first and second boundary, however, for clarity these
reflected rays have been omitted from the diagram.
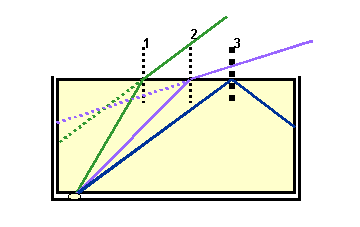
9.b. To an observer the light appears to originate from where the broken
rays cross. This produces a virtual image of the lamp at the apparently
shallower depth.
Note: Some internal reflection occurs for the light incident at
the first and second boundary, however, for clarity these
reflected rays have been omitted from the diagram.
9.b. To an observer the light appears to originate from where the broken
rays cross. This produces a virtual image of the lamp at the apparently
shallower depth.
 10.a.i.
10.a.i.
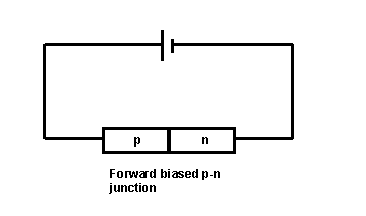 a.ii. When forward biased the majority charge carriers in the n-type
material, electrons, flow to the p-type material. This movement
of electrons also makes it appear that holes in the p-type material
move towards the n-type material.
a.iii.When conduction band electrons in the n-type material pass into the
p-type material they fall into lower energy holes and emit energy as
as a visible photon, if the energy loss is equal to the energy of
a visible photon.
b.i Conduction starts when the applied voltage is 0.5V.
b.ii. The resistance of the diode decreases as the applied voltage
increases. This can be justified by using ohms law to calculate
the resistance at different applied voltages.
R = V/I
R1 = V1/I1
R1 = 1.0/0.275
R1 = 3.6W
R2 = V2/I2
R2 = 1.2/0.5
R2 = 2.4W
11.a. The reaction is an example of nuclear fusion.
b. The total mass of the products from the fusion reaction is less
than the mass of the initial reactants. The difference in mass
is converted into energy. The amount of energy produced can be
calculated using the equation: E = mc2, where m is the
difference in mass and c is the speed of light.
c. Mreactants = (5.00890x10-27+3.34441x10-27)kg
Mreactants = 8.35331x10-27kg
Mproducts = (6.64632x10-27+1.67490x10-27)kg
Mproducts = 8.32122x10-27kg
Mass defect = Mreactants - Mproducts
Mass defect = 8.35331x10-27 - 8.32122x10-27
Mass defect = 0.03209x10-27kg
E = Mdefectc2
E = 0.03209x10-27 x (3x108)2
E = 2.8881x10-12J
d. Number of reactions = Total energy per second/energy per reaction
Number of reactions = 25x106/2.8881x10-12
Number of reactions = 8.658x1018
a.ii. When forward biased the majority charge carriers in the n-type
material, electrons, flow to the p-type material. This movement
of electrons also makes it appear that holes in the p-type material
move towards the n-type material.
a.iii.When conduction band electrons in the n-type material pass into the
p-type material they fall into lower energy holes and emit energy as
as a visible photon, if the energy loss is equal to the energy of
a visible photon.
b.i Conduction starts when the applied voltage is 0.5V.
b.ii. The resistance of the diode decreases as the applied voltage
increases. This can be justified by using ohms law to calculate
the resistance at different applied voltages.
R = V/I
R1 = V1/I1
R1 = 1.0/0.275
R1 = 3.6W
R2 = V2/I2
R2 = 1.2/0.5
R2 = 2.4W
11.a. The reaction is an example of nuclear fusion.
b. The total mass of the products from the fusion reaction is less
than the mass of the initial reactants. The difference in mass
is converted into energy. The amount of energy produced can be
calculated using the equation: E = mc2, where m is the
difference in mass and c is the speed of light.
c. Mreactants = (5.00890x10-27+3.34441x10-27)kg
Mreactants = 8.35331x10-27kg
Mproducts = (6.64632x10-27+1.67490x10-27)kg
Mproducts = 8.32122x10-27kg
Mass defect = Mreactants - Mproducts
Mass defect = 8.35331x10-27 - 8.32122x10-27
Mass defect = 0.03209x10-27kg
E = Mdefectc2
E = 0.03209x10-27 x (3x108)2
E = 2.8881x10-12J
d. Number of reactions = Total energy per second/energy per reaction
Number of reactions = 25x106/2.8881x10-12
Number of reactions = 8.658x1018
Return to past paper index page.




